题目内容
给出下列四个命题,其中不正确命题的序号是______.
①若cosα=cosβ,则α-β=2kπ,k∈Z;②函数y=2cos(2x+
)的图象关于x=
对称;③函数y=cos(sinx)(x∈R)为偶函数,④函数y=sin|x|是周期函数,且周期为2π.
①若cosα=cosβ,则α-β=2kπ,k∈Z;②函数y=2cos(2x+
| π |
| 3 |
| π |
| 12 |
若cosα=cosβ,则α-β=2kπ,或α+β=2kπ,k∈Z,故①不正确;
函数y=2cos(2x+
)的图象关于(
,0)中心对称,故②不正确;
由函数f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)为偶函数,故③正确;
函数y=sin|x|是周期函数,且周期为π,故④不正确.
故答案为:①②④
函数y=2cos(2x+
| π |
| 3 |
| π |
| 12 |
由函数f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)为偶函数,故③正确;
函数y=sin|x|是周期函数,且周期为π,故④不正确.
故答案为:①②④

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目


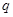 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与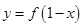 图像关于
图像关于 对称.
对称.