题目内容
已知函数f(x)=sinx+acosx的一个零点是 .
.
(Ⅰ)求实数a的值;
(Ⅱ)设g(x)=[f(x)]2-2sin2x,求g(x)的单调递增区间.
解:(Ⅰ)∵f(x)=sinx+acosx,且 ,
,
∴ ,
,
即 ,解之得a=1.
,解之得a=1.
(Ⅱ)由(Ⅰ)得 f(x)=sinx+cosx.
∴g(x)=[f(x)]2-2sin2x
=(sinx+cosx)2-2sin2x=sin2x+cos2x=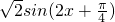 .
.
解不等式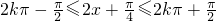 ,
,
得 ,k∈Z.
,k∈Z.
∴函数g(x)的单调递增区间为 ,k∈Z.
,k∈Z.
分析:(I)根据函数解析式,得f( )=
)= ,将sin
,将sin =
= 、cos
、cos =-
=- 代入,即可解出a的值;
代入,即可解出a的值;
(II)由(Ⅰ)得 f(x)=sinx+cosx,由二倍角的余弦公式和辅助角公式,化简整理得g(x)=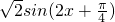 ,结合正弦函数的单调性,解关于x的不等式即可得到求g(x)的单调递增区间.
,结合正弦函数的单调性,解关于x的不等式即可得到求g(x)的单调递增区间.
点评:本题给出三角函数式,求实数a的值并求函数的单调区间,着重考查了三角恒等变换、不等式的解法和三角函数的图象与性质等知识,属于基础题.
 ,
,∴
 ,
,即
 ,解之得a=1.
,解之得a=1. (Ⅱ)由(Ⅰ)得 f(x)=sinx+cosx.
∴g(x)=[f(x)]2-2sin2x
=(sinx+cosx)2-2sin2x=sin2x+cos2x=
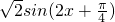 .
.解不等式
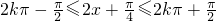 ,
,得
 ,k∈Z.
,k∈Z.∴函数g(x)的单调递增区间为
 ,k∈Z.
,k∈Z.分析:(I)根据函数解析式,得f(
 )=
)= ,将sin
,将sin =
= 、cos
、cos =-
=- 代入,即可解出a的值;
代入,即可解出a的值;(II)由(Ⅰ)得 f(x)=sinx+cosx,由二倍角的余弦公式和辅助角公式,化简整理得g(x)=
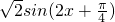 ,结合正弦函数的单调性,解关于x的不等式即可得到求g(x)的单调递增区间.
,结合正弦函数的单调性,解关于x的不等式即可得到求g(x)的单调递增区间.点评:本题给出三角函数式,求实数a的值并求函数的单调区间,着重考查了三角恒等变换、不等式的解法和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
