题目内容
不等式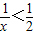 的解集是 .
的解集是 .
【答案】分析:根据x大于0和x小于0分两种情况考虑,当x大于0时,去分母得到不等式的解集,与x大于0求出交集即为原不等式的解集;当x小于0时,去分母得到不等式的解集,与x小于0求出交集即为原不等式的解集,综上,得到所有满足题意的x的范围即为原不等式的解集.
解答:解:当x>0时,去分母得:x>2,
所以原不等式的解集为:(2,+∞);
当x<0时,去分母得:x<2,
所以原不等式的解集为:(-∞,0),
综上,原不等式的解集为:(-∞,0)∪(2,+∞).
故答案为:(-∞,0)∪(2,+∞)
点评:此题考查了其他不等式的解法,考查了分类讨论的数学思想,是一道基础题.学生做题时注意在不等式两边都乘以或除以同一个负数时,不等号要改变.
解答:解:当x>0时,去分母得:x>2,
所以原不等式的解集为:(2,+∞);
当x<0时,去分母得:x<2,
所以原不等式的解集为:(-∞,0),
综上,原不等式的解集为:(-∞,0)∪(2,+∞).
故答案为:(-∞,0)∪(2,+∞)
点评:此题考查了其他不等式的解法,考查了分类讨论的数学思想,是一道基础题.学生做题时注意在不等式两边都乘以或除以同一个负数时,不等号要改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目