题目内容
设有两个集合A={x|
+1≥0,x∈R},B={x|2ax<a+x,a>
,x∈R}.若A∪B=B,求a的取值范围.
| 3-2x |
| x-1 |
| 1 |
| 2 |
分析:把闪光灯两个集合整理成最简形式,一个是分式不等式需要通分整理,根据两个集合的并集的关系得到两个集合的包含关系.得到结果.
解答:解:集合A={x|
+1≥0,x∈R}={x|
≥0}={x|1≤x≤2}
B={x|2ax<a+x,a>
,x∈R}={x|x<
}
∵A∪B=B,
∴A⊆B,
∴
>2,
∴
-2>0
∴
>0
∴
<a<
即当A∪B=B,a的取值范围是
<a<
.
| 3-2x |
| x-1 |
| 2-x |
| x-1 |
B={x|2ax<a+x,a>
| 1 |
| 2 |
| a |
| 2a-1 |
∵A∪B=B,
∴A⊆B,
∴
| a |
| 2a-1 |
∴
| a |
| 2a-1 |
∴
| 2-3a |
| 2a-1 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
即当A∪B=B,a的取值范围是
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查两个集合之间的关系,本题解题的关键是把两个集合整理成最简形式,根据两个集合之间的关系确定两个集合的数值的关系,本题是一个中档题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. (其中a>0,b>0).
(其中a>0,b>0).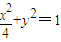 ,求a,b的值.
,求a,b的值. .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;