题目内容
已知函数
，
（
为常数），直线
与函数
、
的图象都相切，且与函数图象的切点的横坐标为
．
（Ⅰ）求直线的方程及的值；
（Ⅱ）若
[注：
是的导函数]，求函数
的单调递增区间；
解：（I）由题意得：与函数y=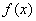
图象的切点为（1，
∵切点（1，在图象上
∴切点为（1，0）
又∵
∴直线的斜率为：
∴直线的x-y-1=0
∵直线与函数y=的图象相切
∴方程组
只有一个解，即方程
∴△=0，解得
(II)由（I）得
∴
∴
又∵
令
∴函数的单调递增区间为
练习册系列答案
相关题目
，求
。
)，则与α终边相同的角的集合是______。 
在
处的切线方程为（ ）
B．
C．
D．
在区间（1，1）上是增函数，则实数a的取值范围是 ．
的展开式的常数项为第（ ）项
B．
C．
D．
满足
,若
的最大值为13,则实数
的值为（ ）
C. 
D. 5
的公差是2，若
成等比数列，则 
等于
B. 
C. 
D. 