题目内容
已知数列{an}是各项均为正数的等比数列，a1+a2=1，a3+a4=4，则a5+a6+a7+a8=（ ）
分析：由等比数列的定义及性质可得，a1+a2，a3+a4，则a5+a6，a7+a8 也成等比数列．结合条件可得a5+a6=16，
a7+a8 =64，从而求得a5+a6+a7+a8 的值．
a7+a8 =64，从而求得a5+a6+a7+a8 的值．
解答：解：由等比数列的定义及性质可得，a1+a2，a3+a4，a5+a6，a7+a8 也成等比数列．
又a1+a2=1，a3+a4=4
故有 a5+a6=16，a7+a8 =64，
∴a5+a6+a7+a8=16+64=80，
故选A．
又a1+a2=1，a3+a4=4
故有 a5+a6=16，a7+a8 =64，
∴a5+a6+a7+a8=16+64=80，
故选A．
点评：本题主要考查等比数列的定义及性质，求得 a5+a6=16，a7+a8 =64，是解题的关键，属于中档题．
练习册系列答案
相关题目
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
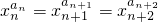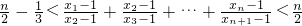（n∈N*）．
．
（n∈N*）．
．
（n∈N*）．
．