Question

实数列满足：，，．

证明不等式

Answer 1

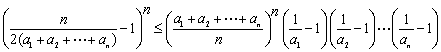
证明：  首先，用数学归纳法证明：．

时，命题显然成立．

假设命题对成立，即有．

设，则是减函数，于是

,

     ，

即命题对n＋1也成立．

原命题等价于．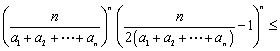

设，则是凸函数，即对，

有．

事实上，等价于

， ．

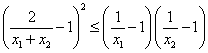所以，由Jenson 不等式可得，

即          ．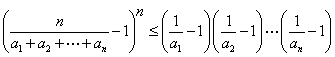

另一方面，由题设及Cauchy不等式，可得

，

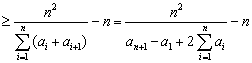
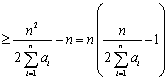所以     ，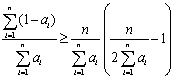

故 

，

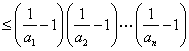从而原命题得证．