题目内容
.有6只电子元件,其中4只正品,两只次品,每次随机抽取一只检验,不论是正品还是次品都不放回,直到两只次品都抽到为止.
(1)求测试4次抽到两只次品的概率;
(2)求2只次品都找到的测试次数ξ的分布列和期望.
(1)求测试4次抽到两只次品的概率;
(2)求2只次品都找到的测试次数ξ的分布列和期望.
分析:(1)设“测试4次抽到两只次品”为事件A,则前3次中只有一次抽到次品,第四次抽到第二只次品,利用古典概型的概率计算公式即可得出;
(2)由题意可知随机变量ξ的可能取值为2,3,4,5,6.利用古典概型的概率计算公式和离散型随机变量的分布列和期望即可得出.
(2)由题意可知随机变量ξ的可能取值为2,3,4,5,6.利用古典概型的概率计算公式和离散型随机变量的分布列和期望即可得出.
解答:解:(1)设“测试4次抽到两只次品”为事件A,则抽4次不放回共有
种方法,其中前3次中只有一次抽到次品且第四次抽到第二只次品的方法为
种方法,
因此P(A)=
=
;
(2)由题意可知随机变量ξ的可能取值为2,3,4,5,6.
则P(ξ=2)=
=
,P(ξ=3)=
=
,P(ξ=4)=
,p(ξ=5)=
=
,P(ξ=5)=
=
.
∴2只次品都找到的测试次数ξ的分布列如表格,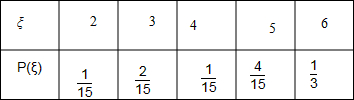
∴Eξ=2×
+3×
+4×
+5×
+6×
=
.
| A | 4 6 |
| C | 1 2 |
| C | 2 4 |
| A | 3 3 |
因此P(A)=
| ||||||
|
| 1 |
| 5 |
(2)由题意可知随机变量ξ的可能取值为2,3,4,5,6.
则P(ξ=2)=
| ||
|
| 1 |
| 15 |
| ||||||
|
| 2 |
| 15 |
| 1 |
| 5 |
| ||||||
|
| 4 |
| 15 |
| ||||||
|
| 1 |
| 3 |
∴2只次品都找到的测试次数ξ的分布列如表格,

∴Eξ=2×
| 1 |
| 15 |
| 2 |
| 15 |
| 1 |
| 15 |
| 4 |
| 15 |
| 1 |
| 3 |
| 14 |
| 3 |
点评:正确理解题意和熟练掌握古典概型的概率计算公式和离散型随机变量的分布列和期望是解题的关键.

练习册系列答案
相关题目