题目内容
已知集合A={a,b,c},其中a,b,c是三个连续的自然数.如果a,b,c能够作为一个三角形的三边长,且该三角形的最大角是最小角的2倍,求所有满足条件的集合A.
(本题满分12分)
解:依题意,不妨设a=n-1,b=n,c=n+1,对应的三个内角是α,π-3α,2α
由正弦定理, …(4分)
…(4分)
所以 …(6分)
…(6分)
由余弦定理,(n-1)2=(n+1)2+n2-2(n+1)ncosα…(8分)
即 化简,得:n2-5n=0
化简,得:n2-5n=0
所以,n=0,或n=5,n=0不合题意,舍去.
n=5,三角形的三边长为4,5,6.…(10分)
可以验证此三角形的最大角是最小角的2倍. …(11分)
故:A={4,5,6} …(12分)
分析:先设出三边长以及三个角的度数,结合正弦定理以及余弦定理求出关于边长的等式,即可求出结论.
点评:本题主要考察正弦定理在解三角形中的应用问题.解决本题的关键在于根据条件得到 化简,得:n2-5n=0,进而求出结论.
化简,得:n2-5n=0,进而求出结论.
解:依题意,不妨设a=n-1,b=n,c=n+1,对应的三个内角是α,π-3α,2α
由正弦定理,
 …(4分)
…(4分)所以
 …(6分)
…(6分)由余弦定理,(n-1)2=(n+1)2+n2-2(n+1)ncosα…(8分)
即
 化简,得:n2-5n=0
化简,得:n2-5n=0所以,n=0,或n=5,n=0不合题意,舍去.
n=5,三角形的三边长为4,5,6.…(10分)
可以验证此三角形的最大角是最小角的2倍. …(11分)
故:A={4,5,6} …(12分)
分析:先设出三边长以及三个角的度数,结合正弦定理以及余弦定理求出关于边长的等式,即可求出结论.
点评:本题主要考察正弦定理在解三角形中的应用问题.解决本题的关键在于根据条件得到
 化简,得:n2-5n=0,进而求出结论.
化简,得:n2-5n=0,进而求出结论. 
练习册系列答案
相关题目
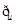 B)=R,则实数a的取值范围是 ( )
B)=R,则实数a的取值范围是 ( )