题目内容
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且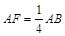 .
.
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)求二面角E-BC1-D的余弦值.
(I)详见解析;(II)二面角E-BC1-D的余弦值为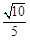 .
.
解析试题分析:(I)由于EF与BD在同一个平面内,显然考虑在ABB1A1这个平面内证明这两条直线平行,这完全就是平面几何的问题了.取AB的中点M, ,所以F为AM的中点,又因为E为
,所以F为AM的中点,又因为E为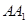 的中点,所以
的中点,所以 .又
.又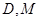 分别为
分别为 的中点,
的中点,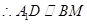 ,且
,且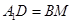 ,所以四边形
,所以四边形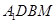 为平行四边形,
为平行四边形,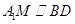 ,
,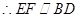 ,由此可得
,由此可得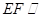 平面
平面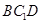 .
.
(II)取AB的中点M,则MB、MC、MD两两垂直,所以可以以M为原点建立空间直角坐标系,利用空间向量求二面角E-BC1-D的余弦值.
试题解析:(I)证明:取AB的中点M, ,所以F为AM的中点,又因为E为
,所以F为AM的中点,又因为E为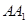 的中点,所以
的中点,所以 .
.
在三棱柱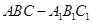 中,
中,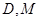 分别为
分别为 的中点,
的中点,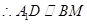 ,且
,且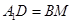 ,
,
所以四边形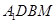 为平行四边形,
为平行四边形,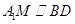 ,
,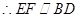 ,又
,又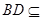 平面
平面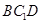 ,
,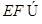 平面
平面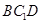 ,
,
所以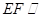 平面
平面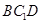 .
.
(II)以AB的中点M为原点,分别以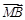 、
、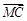 、
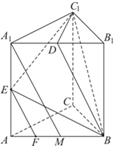
、 所在直线为x轴、y轴、z轴,建立空间直角坐标系如图所示,
所在直线为x轴、y轴、z轴,建立空间直角坐标系如图所示,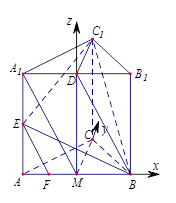
则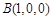 ,
,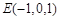 ,
,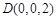 ,
,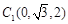 ,
,
∴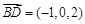 ,
,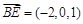 ,
, .
.
设面BC1D的一个法向量为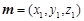 ,面BC1E的一个法向量为
,面BC1E的一个法向量为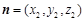 ,
,
则由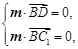 得
得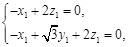 取
取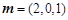 ,
,
又由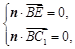 得
得 取
取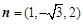 ,
,
则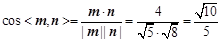 ,
,
故二面角E-BC1-D的余弦值为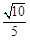 . 12分
. 12分
考点:1、空间直线与平面的位置关系;2、空间向量的应用;3、二面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与
与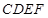 均为正方形,平面
均为正方形,平面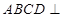 平面
平面
 平面
平面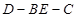 的大小.
的大小.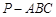 中,点
中,点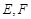 分别是棱
分别是棱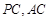 的中点.
的中点.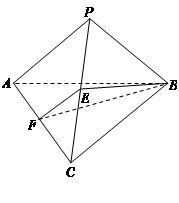
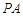 //平面
//平面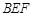 ;
;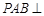 平面
平面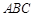 ,
,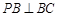 ,求证:
,求证: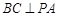 .
. 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且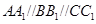 ,
,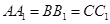 .
.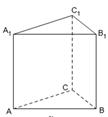
 //平面
//平面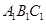 ;
;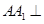 平面
平面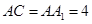 ,
,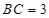 ,
,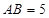 ,求证:
,求证: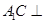 平面
平面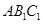 ;
;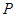 为
为 上的动点,求当
上的动点,求当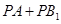 取得最小值时
取得最小值时 的长.
的长.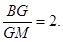
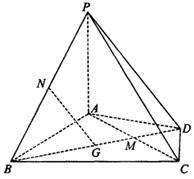
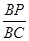 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.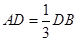 ,点C为圆O上一点,且
,点C为圆O上一点,且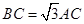 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.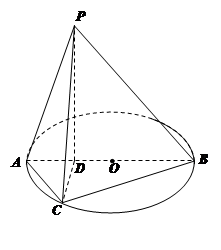
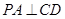 ;
;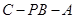 的余弦值.
的余弦值.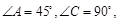
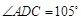 ,
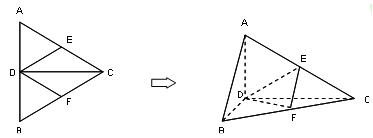
,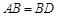 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD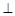 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

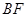 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值.  中,底面
中,底面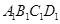 是正方形,
是正方形, 是
是 的中点,
的中点,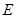 是棱
是棱 上任意一点.
上任意一点.
 ;
; ,求
,求