题目内容
已知 .
.
(1)求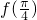 的值;
的值;
(2)若 的值域;
的值域;
(3)求y=f(-x)的单调递增区间.
解:(1)∵
=
=
=2sin(2x+ )+2.
)+2.
∴
=2cos +2
+2
= .
.
(2)若 ,
,
则 ,
,
∴ 时,f(x)min=-2+2=0,
时,f(x)min=-2+2=0,
 时,f(x)max=1+2=3,
时,f(x)max=1+2=3,
∴f(x)的值域是[0,3].
(3)y=f(-x)=2sin(-2x+ )+2,
)+2,
其增区间为:- ≤-2x+
≤-2x+ ≤
≤ ,k∈Z,
,k∈Z,
解得 ,k∈Z,
,k∈Z,
∴y=f(-x)的单调递增区间是[ ,
, ],k∈Z.
],k∈Z.
分析:(1)先由二倍角公式把 等价转化为f(x)=
等价转化为f(x)= ,再由三角函数和(差)公式进一步转化为f(x)=2sin(2x+
,再由三角函数和(差)公式进一步转化为f(x)=2sin(2x+ )+2.由此能求出
)+2.由此能求出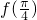 的值.
的值.
(2)若 ,则
,则 ,由此能求出f(x)的值域.
,由此能求出f(x)的值域.
(3)y=f(-x)=2sin(-2x+ )+2,其增区间为:-
)+2,其增区间为:- ≤-2x+
≤-2x+ ≤
≤ ,k∈Z,由此能求了出结果.
,k∈Z,由此能求了出结果.
点评:本题考查解三角函数恒等变换的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意二倍角公式和三角函数和(差)公式的灵活运用.

=

=

=2sin(2x+
 )+2.
)+2.∴

=2cos
 +2
+2=
 .
.(2)若
 ,
,则
 ,
,∴
 时,f(x)min=-2+2=0,
时,f(x)min=-2+2=0, 时,f(x)max=1+2=3,
时,f(x)max=1+2=3,∴f(x)的值域是[0,3].
(3)y=f(-x)=2sin(-2x+
 )+2,
)+2,其增区间为:-
 ≤-2x+
≤-2x+ ≤
≤ ,k∈Z,
,k∈Z,解得
 ,k∈Z,
,k∈Z,∴y=f(-x)的单调递增区间是[
 ,
, ],k∈Z.
],k∈Z.分析:(1)先由二倍角公式把
 等价转化为f(x)=
等价转化为f(x)= ,再由三角函数和(差)公式进一步转化为f(x)=2sin(2x+
,再由三角函数和(差)公式进一步转化为f(x)=2sin(2x+ )+2.由此能求出
)+2.由此能求出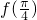 的值.
的值.(2)若
 ,则
,则 ,由此能求出f(x)的值域.
,由此能求出f(x)的值域.(3)y=f(-x)=2sin(-2x+
 )+2,其增区间为:-
)+2,其增区间为:- ≤-2x+
≤-2x+ ≤
≤ ,k∈Z,由此能求了出结果.
,k∈Z,由此能求了出结果.点评:本题考查解三角函数恒等变换的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意二倍角公式和三角函数和(差)公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ·cosθ=1,θ∈(0,π),求θ的值.
·cosθ=1,θ∈(0,π),求θ的值. .
. 的值;
的值; ,求
,求 的值.
的值.
 的值;
的值; 对称,且t∈(0,π),求t的值.
对称,且t∈(0,π),求t的值. 所对的分别是
所对的分别是 。已知
。已知 。(1)求
。(1)求 的值;
的值; 的值。
的值。 .
. 的值;
的值; 的值.
的值.