题目内容
求值:?(1)![]() ;?
;?
(2)lg5·lg20+lg22;?
(3)已知log23=a,3 b=7,求log1256的值.?
解:(1)(2)严格按照指数、对数的运算法则计算,(3)先将3 b=7转化为log37=b,然后设法将log1256化成关于log23和log37的表达式即可求值.?
(1) ![]() =
=![]() =
=![]() .
.
(2)lg5·lg20+lg22=lg5(lg4+lg5)+lg22=2lg2·lg5+lg25+lg22=(lg2+lg5) 2=1.?
(3)解法一:
∵log23=a,∴2 a=3.
又3 b=7,∴7=(2 a) b=2 ab.
故56=2 3+ab.
又12=3·4=2 a·4=2 a+2,
从而![]() .故
.故![]() .
.
解法二:
∵![]() ,∴
,∴![]() .
.
又3 b=7,∴log 37=b.从而![]() =
=![]() =
=![]() =
=![]() =
=
 =
=![]() .
.
解法三:
∵log23=![]() =a,∴lg3=alg2.
=a,∴lg3=alg2.
又3 b=7,∴lg7=blg3.
∴lg7=ablg2.从而log1256=![]() =
=![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目
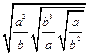 ,其中
,其中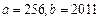 ;
;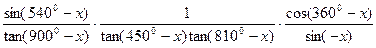
 ,求值:
,求值: ;
; 