题目内容
(本小题满分12分)(注意:在试题卷上作答无效)

如图,在四棱锥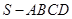 中,底面
中,底面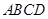 为平行四边形,侧面
为平行四边形,侧面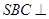 底面
底面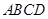 .已知
.已知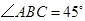 ,
,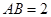 ,
,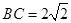 ,
,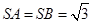 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求直线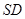 与平面
与平面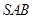 所成角的大小.
所成角的大小.
【答案】
:解法一:(Ⅰ)作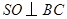 ,垂足为
,垂足为 ,连结
,连结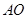 ,由侧面
,由侧面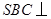 底面
底面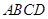 ,得
,得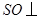 底面
底面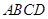 .因为
.因为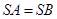 ,所以
,所以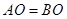 ,
,
又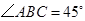 ,故
,故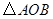 为等腰直角三角形,
为等腰直角三角形,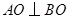 ,由三垂线定理,得
,由三垂线定理,得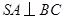 .
.
(Ⅱ)由(Ⅰ)知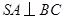 ,依题设
,依题设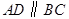 ,
,
故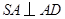 ,由
,由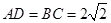 ,
,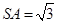 ,
,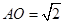 ,得
,得
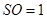 ,
,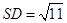 .
.
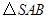 的面积
的面积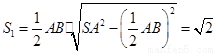 .
.
连结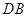 ,得
,得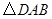 的面积
的面积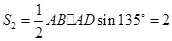
设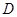 到平面
到平面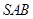 的距离为
的距离为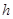 ,由于
,由于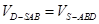 ,得
,得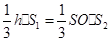 ,解得
,解得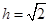 .
.
设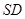 与平面
与平面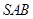 所成角为
所成角为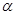 ,则
,则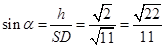 .
.
 所以,直线
所以,直线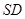 与平面
与平面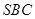 所成的我为
所成的我为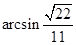 .
.
解法二:
(Ⅰ)作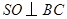 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面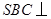 底面
底面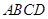 ,得
,得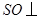 平面
平面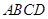 .因为
.因为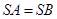 ,所以
,所以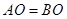 .又
.又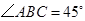 ,
,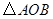 为等腰直角三角形,
为等腰直角三角形,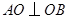 .如图,以
.如图,以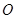 为坐标原点,
为坐标原点,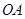 为
为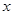 轴正向,建立直角坐标系
轴正向,建立直角坐标系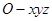 ,
,
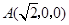 ,
,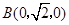 ,
,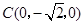 ,
,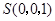 ,
,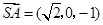 ,
,
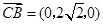 ,
,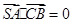 ,所以
,所以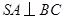 .
.
(Ⅱ)取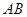 中点
中点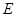 ,
,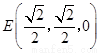 ,连结
,连结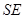 ,取
,取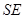 中点
中点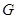 ,连结
,连结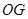 ,
,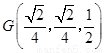 .
.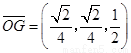 ,
,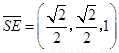 ,
, .
.
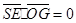 ,
,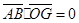 ,
,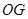 与平面
与平面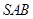 内两条相交直线
内两条相交直线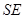 ,
,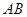 垂直.
垂直.
所以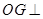 平面
平面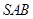 ,
,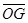 与
与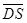 的夹角记为
的夹角记为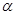 ,
,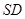 与平面
与平面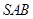 所成的角记为
所成的角记为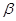 ,则
,则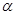 与
与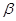 互余.
互余.
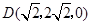 ,
,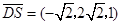 .
. ,
,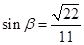 ,
,
所以,直线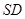 与平面
与平面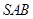 所成的角为
所成的角为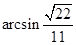
【解析】略

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目