题目内容

【题目】在平面直角坐标系中，不等式组 （r为常数）表示的平面区域的面积为π，若x，y满足上述约束条件，则z= 的最小值为（ ）
A.﹣1
B.﹣
C.
D.﹣

【答案】D
【解析】解：∵不等式组 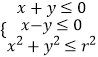（r为常数）表示的平面区域的面积为π， ∴圆x2+y2=r2的面积为4π，则r=2．
由约束条件作出可行域如图，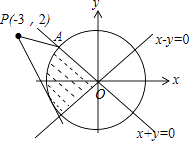

z= =1+ ，
而 的几何意义为可行域内的动点与定点P（﹣3，2）连线的斜率．
设过P的圆的切线的斜率为k，则切线方程为y﹣2=k（x+3），即kx﹣y+3k+2=0．
由 ，解得k=0或k=﹣ ．
∴z= 的最小值为1﹣ ．
故选：D．
由约束条件作出可行域，由z= =1+ ，而 的几何意义为可行域内的动点与定点P（﹣3，2）连线的斜率．结合直线与圆的位置关系求得答案．

练习册系列答案
相关题目

【题目】已知不等式组表示的平面区域为，若函数的图象上存在区域内的点，则实数的取值范围是（ ）

A. B. C. D.

【题目】已知函数f（x）=ax（a＞0，a≠1）的反函数的图象经过点（ ， ）．若函数g（x）的定义域为R，当x∈[﹣2，2]时，有g（x）=f（x），且函数g（x+2）为偶函数，则下列结论正确的是（ ）
A.g（π）＜g（3）＜g（ ）
B.g（π）＜g（ ）＜g（3）??
C.g（ ）＜g（3）＜g（π）
D.g（ ）＜g（π）＜g（3）

【题目】如图所示，四棱锥中，底面，，，，，，为的中点.

（1）求证：平面；

（2）求直线与平面所成角的正弦值.

【题目】过双曲线 的右支上的一点P作一直线l与两渐近线交于A、B两点，其中P是AB的中点；
（1）求双曲线的渐近线方程；
（2）当P坐标为（x0 ， 2）时，求直线l的方程；
（3）求证：|OA||OB|是一个定值．

【题目】已知函数f（x）=e2x﹣ax2+bx﹣1，其中a，b∈R，e为自然对数的底数，若f（1）=0，f′（x）是f（x）的导函数，函数f′（x）在区间（0，1）内有两个零点，则a的取值范围是（ ）
A.（e2﹣3，e2+1）
B.（e2﹣3，+∞）
C.（﹣∞，2e2+2）
D.（2e2﹣6，2e2+2）

【题目】已知等差数列{an}的前n项和为Sn ， 若Sm﹣1=﹣4，Sm=0，Sm+2=14（m≥2，且m∈N*）．
（1）求m的值；
（2）若数列{bn}满足 =logabn（n∈N*），求数列{（an+6）bn}的前n项和．

【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c，已知a≠b，c= ，且bsinB﹣asinA= acosA﹣ bcosB．
（Ⅰ）求C；
（Ⅱ）若△ABC的面积为 ，求a与b的值．

【题目】已知椭圆C：（a＞b＞0）的两个焦点分别为F1，F2，离心率为，过F1的直线l与椭圆C交于M，N两点，且△MNF2的周长为8．

（1）求椭圆C的方程；

（2）若直线y＝kx＋b与椭圆C分别交于A，B两点，且OA⊥OB，试问点O到直线AB的距离是否为定值，证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网