题目内容
已知函数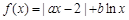 (x>0).
(x>0).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程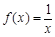 在(0,1]上解的个数.
在(0,1]上解的个数.
【答案】
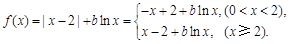
1/当0<x<2时,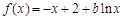 ,
,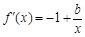 .由条件,得
.由条件,得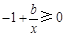 恒成立,
恒成立,
即b≥x恒成立.∴b≥2. …………… 2分
② 当x≥2时, ,
,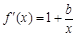 .由条件,得
.由条件,得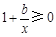 恒成立,
恒成立,
即b≥-x恒成立.∴b≥-2.…………… 4分
综合①,②得b的取值范围是b≥2. …………………… 5分
(2)令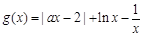 ,即
,即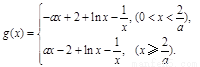
当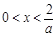 时,
时,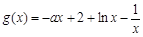 ,.
,.
∵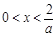 ,∴
,∴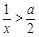 .则
.则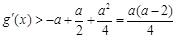 ≥0.
≥0.
即 ,∴
,∴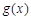 在(0,
在(0, )上是递增函数. ………………… 7分
)上是递增函数. ………………… 7分
当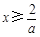 时,
时,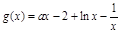 ,
,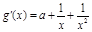 >0.∴
>0.∴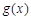 在(
在( ,+∞)上是递增函数.又因为函数g(x)在
,+∞)上是递增函数.又因为函数g(x)在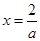 有意义,∴
有意义,∴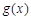 在(0,+∞)上是递增函数.…… 10分
在(0,+∞)上是递增函数.…… 10分
∵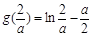 ,而a≥2,∴
,而a≥2,∴ ,则
,则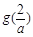 <0.∵a≥2,∴
<0.∵a≥2,∴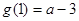 ……
12分
……
12分
当a≥3时,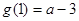 ≥0,∴g(x)=0在
≥0,∴g(x)=0在 上有惟一解.当
上有惟一解.当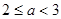 时,
时,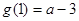 <0,∴g(x)=0在
<0,∴g(x)=0在 上无解
上无解
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
