题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,丨φ丨<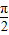 的图象与y 轴交点的纵坐标为1,在相邻的两点(x,2),(x
的图象与y 轴交点的纵坐标为1,在相邻的两点(x,2),(x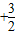 ,-2)(x>0)上f(x)分别取得最大值和最小值.
,-2)(x>0)上f(x)分别取得最大值和最小值.(1)求f(x)的解析式;
(2)若函数g(x)=af(x)+b的最大和最小值分别为6和2,求a,b的值.
【答案】分析:(1)依题意,得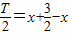 ,解得T,再利用T=
,解得T,再利用T=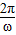 ,解得ω.又最大值为2,最小值为-2,可得A=2,于是y=
,解得ω.又最大值为2,最小值为-2,可得A=2,于是y=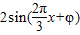 .根据图象经过(0,1),可得2sinφ=1,又|φ|
.根据图象经过(0,1),可得2sinφ=1,又|φ|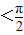 ,可得φ.
,可得φ.
(2)利用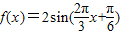 .和-2≤f(x)≤2,即可得出
.和-2≤f(x)≤2,即可得出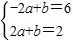 或
或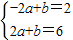 解出即可.
解出即可.
解答:解:(1)依题意,得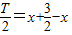 ,解得T=3=
,解得T=3=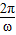 ,解得ω=
,解得ω=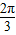 .
.
∵f(x)的最大值为2,最小值为-2,∴A=2,
∴y=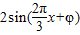 .
.
∵图象经过(0,1),
∴2sinφ=1,即sinφ= .
.
又|φ|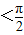 ,∴φ=
,∴φ=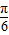 ,∴
,∴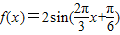 .
.
(2)∵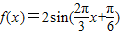 .
.
∴-2≥f(x)≤2,
∴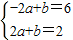 或
或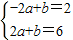
解得,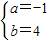 或
或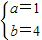
点评:熟练掌握三角函数的图象与性质是解题的关键.
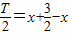 ,解得T,再利用T=
,解得T,再利用T=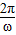 ,解得ω.又最大值为2,最小值为-2,可得A=2,于是y=
,解得ω.又最大值为2,最小值为-2,可得A=2,于是y=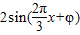 .根据图象经过(0,1),可得2sinφ=1,又|φ|
.根据图象经过(0,1),可得2sinφ=1,又|φ|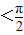 ,可得φ.
,可得φ.(2)利用
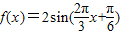 .和-2≤f(x)≤2,即可得出
.和-2≤f(x)≤2,即可得出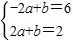 或
或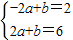 解出即可.
解出即可.解答:解:(1)依题意,得
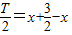 ,解得T=3=
,解得T=3=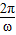 ,解得ω=
,解得ω=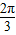 .
.∵f(x)的最大值为2,最小值为-2,∴A=2,
∴y=
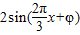 .
.∵图象经过(0,1),
∴2sinφ=1,即sinφ=
 .
.又|φ|
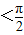 ,∴φ=
,∴φ=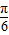 ,∴
,∴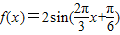 .
.(2)∵
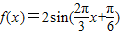 .
.∴-2≥f(x)≤2,
∴
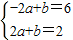 或
或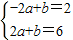
解得,
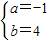 或
或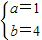
点评:熟练掌握三角函数的图象与性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目