题目内容
如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,
底面![]() 是菱形,且
是菱形,且![]() ,
,![]() 为
为![]() 的中点.(Ⅰ)证明:
的中点.(Ⅰ)证明:![]() 平面
平面![]() ; (Ⅱ)侧棱
; (Ⅱ)侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?
?
并证明你的结论.
(Ⅰ)略(Ⅱ)![]() 为侧棱
为侧棱![]() 的中点
的中点
解析:
:证明:(Ⅰ) ![]() 是菱形,
是菱形,![]() ,
,
![]() ,
,
![]() 为正三角形,……2分
为正三角形,……2分
又![]() 为
为![]() 的中点,
的中点,![]()
![]()
![]() ,则有
,则有![]() ,
,![]() ,
,
![]() ,
,![]() 4分 又
4分 又![]() ,
,
![]() 底面
底面![]() ,
,![]() 由
由![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() …7分
…7分
(Ⅱ)![]() 为侧棱
为侧棱![]() 的中点时,
的中点时,![]() 平面
平面![]() .……8分
.……8分
证法一:设![]() 为
为![]() 的中点,连
的中点,连![]() ,则
,则![]() 是
是![]() 的中位线,
的中位线,
![]() 且
且![]() ,又
,又![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为平行四边形, ……………11分
为平行四边形, ……………11分
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
. ![]() ………………14分
………………14分
证法二:设![]() 为
为![]() 的中点,连
的中点,连![]() ,则
,则![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() . …10分
. …10分
同理,由![]() ,得
,得![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,………12分
,………12分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .………14分
.………14分

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
 如图,在四棱锥
如图,在四棱锥
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.
 平面EDB;
平面EDB; 中,底面
中,底面 为菱形,
为菱形, ,
,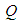 为
为 的中点。
的中点。
 ,求证:平面
,求证:平面 ;
; 在线段
在线段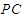 上,
上, ,试确定
,试确定 的值,使
的值,使 ;
; 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面 为AD的中点,
为AD的中点, 是棱
是棱 上的点,
上的点, ,
, .(1)若
.(1)若
 ;(2)求证:平面
;(2)求证:平面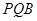 ⊥平面
⊥平面