题目内容
椭圆C:  +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=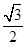 ,a+b=3.
,a+b=3.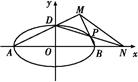
(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明2m-k为定值.
(1)  +y2=1 (2)见解析
+y2=1 (2)见解析
解析(1)解:因为e=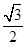 =
= ,
,
所以a=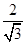 c,b=
c,b=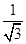 c.
c.
代入a+b=3,
得c= ,a=2,b=1.
,a=2,b=1.
故椭圆C的方程为 +y2=1.
+y2=1.
(2)证明:因为B(2,0),P不为椭圆顶点,
则直线BP的方程为y=k(x-2)(k≠0,k≠± ), ①
), ①
把①代入 +y2=1,
+y2=1,
解得P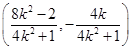 .
.
直线AD的方程为y= x+1.②
x+1.②
①与②联立解得M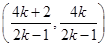 .
.
由D(0,1),P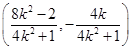 ,N(x,0)三点共线知
,N(x,0)三点共线知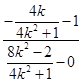 =
=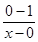 ,
,
解得N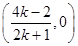 .
.
所以MN的斜率为m=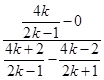
=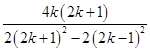
=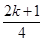 ,
,
则2m-k=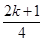 -k=
-k= (定值).
(定值).

练习册系列答案
相关题目
 直线
直线 与抛物线
与抛物线 没有交点;
没有交点; 方程
方程 表示椭圆;若
表示椭圆;若 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围.

 |AB|,求椭圆的方程.
|AB|,求椭圆的方程. 、
、 (
( )连线的斜率之积等于非零常数m的点的轨迹,加上
)连线的斜率之积等于非零常数m的点的轨迹,加上 、
、 两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.
两点所成的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m值得关系.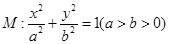 的离心率为
的离心率为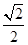 ,且过点
,且过点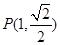 直线
直线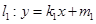 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线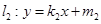 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形