题目内容
20．在直角坐标系xoy中，锐角α的顶点为坐标原点，始边在x轴的非负半轴上，角α的终边与单位圆交于点P（$\frac{2\sqrt{5}}{5}$，y）．（Ⅰ）求sinα和cosα的值；
（Ⅱ）求$\frac{sinα+cosα}{sinα-cosα}$的值．
分析 （Ⅰ）根据P坐标求出P到原点O的距离，利用任意角三角函数定义求出sinα和cosα的值即可；
（Ⅱ）把求出的sinα与cosα的值代入原式计算即可得到结果．
解答 解：（Ⅰ）由题意得$\sqrt{（\frac{2\sqrt{5}}{5}）^{2}+{y}^{2}}$=1，
解得：y=±$\frac{\sqrt{5}}{5}$，
∵α是锐角，∴y=$\frac{\sqrt{5}}{5}$，
则sinα=$\frac{\sqrt{5}}{5}$，cosα=$\frac{2\sqrt{5}}{5}$；
（Ⅱ）∵则sinα=$\frac{\sqrt{5}}{5}$，cosα=$\frac{2\sqrt{5}}{5}$，
∴原式=$\frac{\frac{\sqrt{5}}{5}+\frac{2\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}-\frac{2\sqrt{5}}{5}}$=-3．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
10．已知$sinx=\frac{{\sqrt{3}}}{5}（\frac{π}{2}＜x＜π）$，则x的值（ ）
| A． | $arcsin\frac{{\sqrt{3}}}{5}$ | B． | arcsin（-$\frac{\sqrt{3}}{5}$） | C． | π-arcsin$\frac{{\sqrt{3}}}{5}$ | D． | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{5}$ |
8．某中学对高二甲、乙两个同类班级，进行“加强‘语文阅读理解’训练，对提高‘数学应用题’得分率作用”的试验，其中甲班为试验班（加强语文阅读理解训练），乙班为对比班（常规教学，无额外训练），在试验前的测试中，甲、乙两班学生在数学应用题上的得分率基本一致，试验结束后，统计几次数学应用题测试的平均成绩（均取整数）如下表所示：
现规定平均成绩在80分以上（不含80分）的为优秀．
（Ⅰ）试分析估计两个班级的优秀率；
（Ⅱ）由以上统计数据填写下面2×2列联表，并问“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”是否有帮助．
参考公式及数据：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，
| 60分以下 | 61～70分 | 71～80分 | 81～90分 | 91～100分 | |
| 甲班（人数） | 3 | 6 | 11 | 18 | 12 |
| 乙班（人数） | 7 | 13 | 10 | 10 | 10 |
（Ⅰ）试分析估计两个班级的优秀率；
（Ⅱ）由以上统计数据填写下面2×2列联表，并问“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”是否有帮助．
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
| P（Χ2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P（Χ2≥k0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15．从同一顶点出发的三条棱长分别为1、1、$\sqrt{2}$的长方体的各顶点均在同一个球面上，则该球的体积为 （ ）
| A． | $\frac{32π}{3}$ | B． | 4π | C． | 2π | D． | $\frac{4π}{3}$ |
5．sin600°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
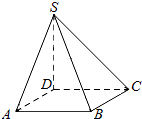如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=2．