题目内容
直三棱柱ABC-A1B1C1中,AB⊥BC,E是A1C的中点,ED⊥A1C且交AC于D,A1A=AB=
BC.
(I)证明:B1C1∥平面A1BC;
(II)证明:A1C⊥平面EDB;
(III)求平面A1AB与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况).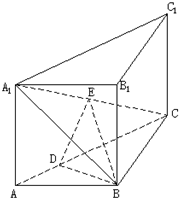
| ||
| 2 |
(I)证明:B1C1∥平面A1BC;
(II)证明:A1C⊥平面EDB;
(III)求平面A1AB与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况).

证明:(I)∵三棱柱ABC-A1B1C1中B1C1∥BC,(1分)
又BC?平面A1BC,且B1C1?平面A1BC,
∴B1C1∥平面A1BC(3分)
(II)∵三棱柱ABC-A1B1C1中A1A⊥AB,
∴Rt△A1AB中AB=
| ||
| 2 |
| ||
| 2 |
∴BC=A1B,
∴△A1BC是等腰三角形(6分)
∵E是等腰△A1BC底边A1C的中点,
∴A1C⊥BE①
又依条件知A1C⊥ED②
且ED∩BE=E③
由①,②,③得A1C⊥平面EDB(8分)
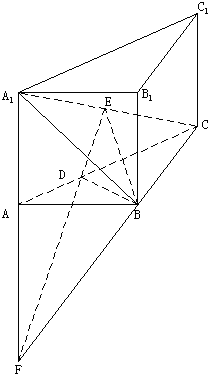
(III)∵A1A、ED?平面A1AC,
且A1A、ED不平行,
故延长A1A,ED后必相交,
设交点为F,连接EF,如图
∴A1-BF-E是所求的二面角(10分)
依条件易证明Rt△A1EF≌Rt△A1AC∵E为A1C中点,
∴A为A1F中点∴AF=A1A=AB
∴∠A1BA=∠ABF=45°
∴∠A1FB=90°
即A1B⊥FB(12分)
又A1E⊥平面EFB,
∴EB⊥FB
∴∠A1BE是所求的二面角的平面角(13分)
∵E为等腰直角三角形A1BC底边中点,
∴∠A1BE=45°
故所求的二面角的大小为45°(14分)

练习册系列答案
相关题目
 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1= 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( ) 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







