题目内容
已知圆C: 关于直线
关于直线 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为
(1)求圆C的方程;
(2)是否存在斜率为2的直线 ,
, 截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出
截圆C所得的弦为AB,且以AB为直径的圆过原点,若存在,则求出 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
(1) (2)满足条件的直线不存在
(2)满足条件的直线不存在
解析试题分析:(1)圆心为 2分
2分
由题意: 4分
4分
解得: 或
或 (舍)
(舍)
圆C的方程为 6分
6分
(2)假设存在满足要求的直线 ,设其方程为
,设其方程为 ,
,
设 ,由题意,
,由题意, 8分
8分
得: (*) 10分
(*) 10分
将 代入圆的方程
代入圆的方程 得:
得: ,该方程的两根为
,该方程的两根为 12分
12分
将 代入 (*)得:
代入 (*)得: 14分
14分 方程无解,满足条件的直线不存在. 16分
方程无解,满足条件的直线不存在. 16分
考点:圆的方程,直线与圆的位置关系
点评:解决的关键是根据直线与圆的位置关系,结合韦达定理来求解分析,属于基础题。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
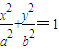 的左、右两个焦点.
的左、右两个焦点. )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标.
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标.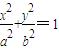 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.