题目内容
已知函数f(x)=ax3+bx2-2(a≠0)有且仅有两个不同的零点x1,x2,则( )A.当a<0时,x1+x2<0,x1x2>0
B.当a<0时,x1+x2>0,x1x2<0
C.当a>0时,x1+x2<0,x1x2>0
D.当a>0时,x1+x2>0,x1x2<0
【答案】分析:求导数可得x=0,或x=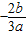 时,函数取得极值,要满足题意需f(
时,函数取得极值,要满足题意需f(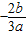 )=0,可得a,b的关系,当a>0时,x1+x2的正负不确定,不合题意;当a<0,可得x1x2<0,x1+x2>0,进而可得答案.
)=0,可得a,b的关系,当a>0时,x1+x2的正负不确定,不合题意;当a<0,可得x1x2<0,x1+x2>0,进而可得答案.
解答: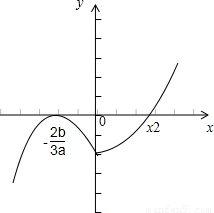 解:原函数的导函数为f′(x)=3ax2+2bx=x(3ax+2b),
解:原函数的导函数为f′(x)=3ax2+2bx=x(3ax+2b),
令f′(x)=0,可解得x=0,或x=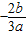 ,
,
故当x=0,或x=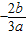 时,函数取得极值,又f(0)=-2<0,
时,函数取得极值,又f(0)=-2<0,
所以要使函数f(x)=ax3+bx2-2(a≠0)有且仅有两个不同的零点,
则必有f(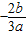 )=a
)=a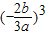 +b
+b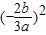 -2=0,解得
-2=0,解得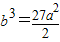 ,且b>0,
,且b>0,
即函数的一根为x1=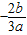 ,
,
(1)如下图,若a>0,可知x1=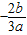 <0,且为函数的极大值点,x=x2处为函数的极小值点,
<0,且为函数的极大值点,x=x2处为函数的极小值点,
此时函数有2个零点: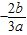 ,x2>0,显然有x1x2<0,但x1+x2的正负不确定,故可排除C,D;
,x2>0,显然有x1x2<0,但x1+x2的正负不确定,故可排除C,D;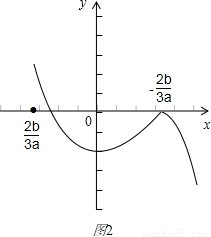
(2)如图2,若a<0,必有x1=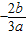 >0,此时必有x1x2<0,x1=
>0,此时必有x1x2<0,x1=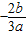 的对称点为x=
的对称点为x=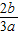 ,
,
则f(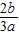 )=a
)=a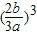 +b
+b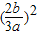 -2=
-2=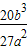 -2=
-2=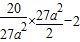 =8>0,
=8>0,
则必有x2>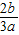 ,即x2-
,即x2-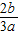 >0,即x1+x2>0
>0,即x1+x2>0
故选B
点评:本题考查根的存在性及根的个数的判断,涉及三次函数的图象以及分类讨论的思想,属中档题
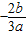 时,函数取得极值,要满足题意需f(
时,函数取得极值,要满足题意需f(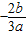 )=0,可得a,b的关系,当a>0时,x1+x2的正负不确定,不合题意;当a<0,可得x1x2<0,x1+x2>0,进而可得答案.
)=0,可得a,b的关系,当a>0时,x1+x2的正负不确定,不合题意;当a<0,可得x1x2<0,x1+x2>0,进而可得答案.解答:
 解:原函数的导函数为f′(x)=3ax2+2bx=x(3ax+2b),
解:原函数的导函数为f′(x)=3ax2+2bx=x(3ax+2b),令f′(x)=0,可解得x=0,或x=
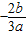 ,
,故当x=0,或x=
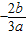 时,函数取得极值,又f(0)=-2<0,
时,函数取得极值,又f(0)=-2<0,所以要使函数f(x)=ax3+bx2-2(a≠0)有且仅有两个不同的零点,
则必有f(
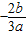 )=a
)=a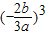 +b
+b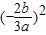 -2=0,解得
-2=0,解得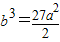 ,且b>0,
,且b>0,即函数的一根为x1=
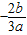 ,
,(1)如下图,若a>0,可知x1=
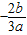 <0,且为函数的极大值点,x=x2处为函数的极小值点,
<0,且为函数的极大值点,x=x2处为函数的极小值点,此时函数有2个零点:
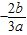 ,x2>0,显然有x1x2<0,但x1+x2的正负不确定,故可排除C,D;
,x2>0,显然有x1x2<0,但x1+x2的正负不确定,故可排除C,D;
(2)如图2,若a<0,必有x1=
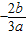 >0,此时必有x1x2<0,x1=
>0,此时必有x1x2<0,x1=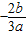 的对称点为x=
的对称点为x=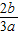 ,
,则f(
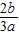 )=a
)=a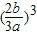 +b
+b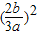 -2=
-2=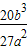 -2=
-2=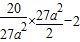 =8>0,
=8>0,则必有x2>
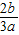 ,即x2-
,即x2-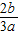 >0,即x1+x2>0
>0,即x1+x2>0故选B
点评:本题考查根的存在性及根的个数的判断,涉及三次函数的图象以及分类讨论的思想,属中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目