Question

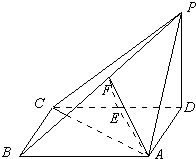如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E、F分别为CD、PB的中点．
（1）求证：EF⊥平面PAB；
（2）设AB=

2

BC，求AC与平面AEF所成的角的正弦值．

Answer 1

分析：（1）先由条件证明BA⊥平面EFG，可得BA⊥EF ①．再求得△EPB为等腰三角形，故有EF⊥BP ②．由①②利用直线和平面垂直的判定定理可得EF⊥平面PAB．
（2）设AD=1=PD，则AB=

2

．设AC∩BD=O，则FO⊥平面ABCD．设点C到平面AEF的距离为h，根据V_F-ACE=V_C-AEF 求得h=

1

2

．而AC=

3

，设AC与平面AEF所成的角为θ，由sinθ=

h

AC

，运算求得结果．

解答：解：（1）∵ABCD为矩形，PD⊥底面ABCD，∴BA⊥PA．
取AB得中点为G，∵E、F分别为CD、PB的中点，∴EG⊥AB．
再由FG为△BAP的中位线，可得FG∥PA，∴FG⊥BA．
这样，BA垂直于平面EFG内的两条相交直线EG、FG，∴BA⊥平面EFG，∴BA⊥EF  ①．
由AD=PD可得EP=

ED2+PD2

=EB=

EC2+BC2

，故△EPB为等腰三角形，故有EF⊥BP ②．
由①②可得EF⊥平面PAB．
（2）设AD=1=PD，则AB=

2

．设AC∩BD=O，则FO为△BPD的中位线，故FO=

1

2

PD=

1

2

，且FO⊥平面ABCD．
设点C到平面AEF的距离为h，∵V_F-ACE=V_C-AEF，∴

1

3

•

1

2

•CE•AD•FO=

1

3

•

1

2

•AF•EF•h．
化简可得，CE•AD•FO=AF•EF•h ③．
再由AE=

AD2+DE2

=

1+ 1 2

=

6

2

，AF=

1

2

BD（直角三角形斜边上的中线等于斜边的一半）=

1

2

PD2+BD2

=

1

2

1+3

=1，
可得EF=

AE2-AF2

=

2

2

．
故由③可得

2

2

×1×

1

2

=1×

2

2

×h，解得h=

1

2

．
而AC=

3

，设 AC与平面AEF所成的角为θ，则sinθ=

h

AC

=

1 2

3

=

3

6

，
故AC与平面AEF所成的角的正弦值为

3

6

．

点评：本题主要考查直线和平面垂直的判定定理的应用，用等体积法求点到平面的距离，直线和平面所成的角的定义和求法，属于中档题．