题目内容
已知函数f(x)=|log2|x||的定义域为[a,b],值域为[0,2],则a+b的取值范围是________.
{-5,- ,5}
,5}
分析:函数f(x)=|log2|x||的定义域为[a,b],值域为[0,2],若1≤|a|<|b|,则log2|a|=0,|a|=1,log2|b|=2,|b|=4;若1≤|b|<|a|,则log2|b|=0,|b|=1,log2|a|=2,|a|=4;若|a|<|b|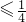 ,log2|a|=0,|a|=1,log2|b|=-2,|b|=
,log2|a|=0,|a|=1,log2|b|=-2,|b|= .由此能够求出a+b的取值范围.
.由此能够求出a+b的取值范围.
解答:∵函数f(x)=|log2|x||的定义域为[a,b],值域为[0,2],
当1≤|a|<|b|时,
则log2|a|=0,|a|=1,
log2|b|=2,|b|=4,
∵0<a<b,
∴a=1,b=4,a+b=5,
当1≤|b|<|a|时,
则log2|b|=0,|b|=1,
log2|a|=2,|a|=4,
∵a<b<0,
∴a=-4,b=-1,a+b=-5.
当|a|<|b|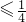 时,
时,
log2|a|=0,|a|=1,
log2|b|=-2,|b|= ,
,
∵a<b<0,
∴a=-1,b=- ,a+b=-
,a+b=- .
.
所以,a+b的取值范围是:{-5,- ,5}.
,5}.
故答案为:{-5,- ,5}.
,5}.
点评:本题考查对数的性质和应用,解题时要认真审题,仔细解答,易错点是考虑问题不够全面,导致丢解.
 ,5}
,5}分析:函数f(x)=|log2|x||的定义域为[a,b],值域为[0,2],若1≤|a|<|b|,则log2|a|=0,|a|=1,log2|b|=2,|b|=4;若1≤|b|<|a|,则log2|b|=0,|b|=1,log2|a|=2,|a|=4;若|a|<|b|
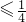 ,log2|a|=0,|a|=1,log2|b|=-2,|b|=
,log2|a|=0,|a|=1,log2|b|=-2,|b|= .由此能够求出a+b的取值范围.
.由此能够求出a+b的取值范围.解答:∵函数f(x)=|log2|x||的定义域为[a,b],值域为[0,2],
当1≤|a|<|b|时,
则log2|a|=0,|a|=1,
log2|b|=2,|b|=4,
∵0<a<b,
∴a=1,b=4,a+b=5,
当1≤|b|<|a|时,
则log2|b|=0,|b|=1,
log2|a|=2,|a|=4,
∵a<b<0,
∴a=-4,b=-1,a+b=-5.
当|a|<|b|
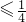 时,
时,log2|a|=0,|a|=1,
log2|b|=-2,|b|=
 ,
,∵a<b<0,
∴a=-1,b=-
 ,a+b=-
,a+b=- .
.所以,a+b的取值范围是:{-5,-
 ,5}.
,5}.故答案为:{-5,-
 ,5}.
,5}.点评:本题考查对数的性质和应用,解题时要认真审题,仔细解答,易错点是考虑问题不够全面,导致丢解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|