题目内容
(2012•宜宾一模)某单位在2011新年联欢会上举行一个抽奖活动:甲箱中装有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
分析:(Ⅰ)设事件A1表示从甲箱中摸出红球,事件A2表示从乙箱中摸出红球,根据题意,易得这两个事件的概率,参加者获奖即A1和A2同时发生,由相互独立事件的概率乘法公式,计算可得答案;
(Ⅱ)设X为5人中获奖的人次,这5人中至少有3人获奖,即包括3人获奖、4人获奖、5人获奖三种情况,由n次独立重复实验中恰有k次发生的概率公式可得每种情况的概率,根据互斥事件概率的加法公式将其相加可得答案.
(Ⅱ)设X为5人中获奖的人次,这5人中至少有3人获奖,即包括3人获奖、4人获奖、5人获奖三种情况,由n次独立重复实验中恰有k次发生的概率公式可得每种情况的概率,根据互斥事件概率的加法公式将其相加可得答案.
解答:解:(Ⅰ)设事件A1表示从甲箱中摸出红球,事件A2表示从乙箱中摸出红球,
因为从甲箱中摸球的结果不影响从乙箱中摸球的结果,所以A1和A2相互独立;
p(A1)=
,p(A2)=
=
,
所以 P(获奖)=P(A1A2)=P(A1)P(A2)=
×
=0.2.
(Ⅱ)设X为5人中获奖的人次,
这5人中至少有3人获奖,即包括3人获奖、4人获奖、5人获奖三种情况,
则P(X≥3)=P(X=3)+P(X=4)+P(X=5)=C53•0.23•(1-0.2)2+C54•0.24•(1-0.2)+C55•0.25=
.
所以,5人中至少有3人获奖的概率为
.
因为从甲箱中摸球的结果不影响从乙箱中摸球的结果,所以A1和A2相互独立;
p(A1)=
| 3 |
| 5 |
| 2 |
| 6 |
| 1 |
| 3 |
所以 P(获奖)=P(A1A2)=P(A1)P(A2)=
| 3 |
| 5 |
| 1 |
| 3 |
(Ⅱ)设X为5人中获奖的人次,
这5人中至少有3人获奖,即包括3人获奖、4人获奖、5人获奖三种情况,
则P(X≥3)=P(X=3)+P(X=4)+P(X=5)=C53•0.23•(1-0.2)2+C54•0.24•(1-0.2)+C55•0.25=
| 181 |
| 3125 |
所以,5人中至少有3人获奖的概率为
| 181 |
| 3125 |
点评:本题考查n次独立重复实验中恰有k次发生的概率与互斥事件概率的加法公式,注意(Ⅱ)中,分情况讨论计算,要细心计算.

练习册系列答案
相关题目
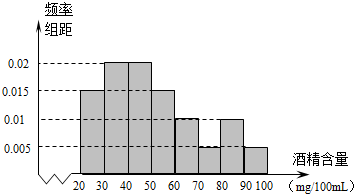 (2012•宜宾一模)《中华人民共和国道路交通安全法》
(2012•宜宾一模)《中华人民共和国道路交通安全法》