题目内容
已知函数f(x)=a(lnx-x)(a∈R).(I)讨论函数f(x)的单调性;
(II)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,函数g(x)=
 在区间(2,3)上总存在极值,求实数m的取值范围.
在区间(2,3)上总存在极值,求实数m的取值范围.
【答案】分析:(I)利用导数研究函数的单调性,首先求出极值点,同时注意函数的定义域;
(II)已知函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,根据导数与直线斜率的关系可得f′(2)=1,将问题转化为二元一次方程有解问题,从而求解;
解答:解:(I)易知f(x)的定义域为(0,+∞),f′(x)=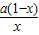 ,
,
当a<0时,令f′(x)=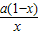 >0,即
>0,即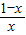 <0,解得增区间为(1,+∞),
<0,解得增区间为(1,+∞),
减区间为(0,1);
当a>0时,令f′(x)=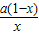 >0,即
>0,即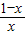 >0,解得增区间为(0,1),减区间为(1,+∞),
>0,解得增区间为(0,1),减区间为(1,+∞),
当a=0时,f(x)不是单调函数;
(II)∵函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
∴f′(2)=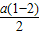 =tan45°=1,
=tan45°=1,
∴a=-2,
f′(x)=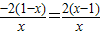 ,
,
g(x)=x3+x2(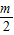 +
+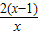 )=x3+(
)=x3+(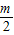 +2)x2-2x,
+2)x2-2x,
g′(x)=3x2+(m+4)x-2,
∵g′(0)=-2<0,要使函数g(x)=x3+x2[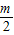 +f′(x)]在区间(2,3)上总存在极值,
+f′(x)]在区间(2,3)上总存在极值,
只需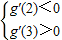 ,
,
解得-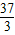 <m<-9;
<m<-9;
点评:此题利用导数研究函数单调区间,以及导数所表示的几何意义,将问题转化为方程有解问题,是一道中档题;
(II)已知函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,根据导数与直线斜率的关系可得f′(2)=1,将问题转化为二元一次方程有解问题,从而求解;
解答:解:(I)易知f(x)的定义域为(0,+∞),f′(x)=
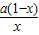 ,
,当a<0时,令f′(x)=
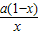 >0,即
>0,即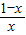 <0,解得增区间为(1,+∞),
<0,解得增区间为(1,+∞),减区间为(0,1);
当a>0时,令f′(x)=
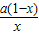 >0,即
>0,即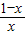 >0,解得增区间为(0,1),减区间为(1,+∞),
>0,解得增区间为(0,1),减区间为(1,+∞),当a=0时,f(x)不是单调函数;
(II)∵函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
∴f′(2)=
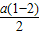 =tan45°=1,
=tan45°=1,∴a=-2,
f′(x)=
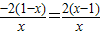 ,
,g(x)=x3+x2(
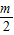 +
+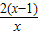 )=x3+(
)=x3+(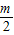 +2)x2-2x,
+2)x2-2x,g′(x)=3x2+(m+4)x-2,
∵g′(0)=-2<0,要使函数g(x)=x3+x2[
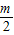 +f′(x)]在区间(2,3)上总存在极值,
+f′(x)]在区间(2,3)上总存在极值,只需
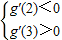 ,
,解得-
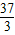 <m<-9;
<m<-9;点评:此题利用导数研究函数单调区间,以及导数所表示的几何意义,将问题转化为方程有解问题,是一道中档题;

练习册系列答案
相关题目