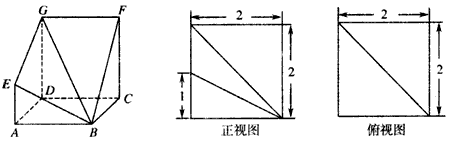
题目内容
如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=1,AB=2,SD= ,
,
(1)求证:CD⊥平面ADS;
(2)求AD与SB所成角的余弦值;
(3)求二面角A-SB-D的余弦值。
 ,
,(1)求证:CD⊥平面ADS;
(2)求AD与SB所成角的余弦值;
(3)求二面角A-SB-D的余弦值。

|
解:(1)∵ABCD是矩形, |
|
| (2)DA、DC、DS两两互相垂直, 建立如图所示的空间直角坐标系, ∴  , , ∴  , ,∴  , , ∴AD与SB所成的角的余弦为  。 。 (3)  , ,设面SBD的一个法向量为  , ,∴  , , 又  , ,∴设面DAB的一个法向量为  , ,∴  , ,∴  , ,所以所求的二面角的余弦为  。 。 |
 |

练习册系列答案
相关题目



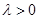 使得
使得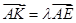 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为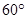 ,求
,求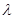 的值。
的值。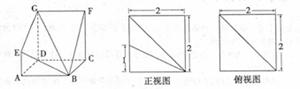
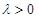 使得
使得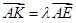 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为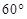 ,求
,求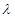 的值。
的值。
 使得
使得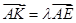 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为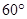 ,求
,求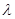 的值。
的值。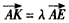 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。