题目内容
已知实数a满足0<a≤2,a≠1,设函数f(x)= x3-
x3- x2+ax.
x2+ax.
(1)当a=2时,求f(x)的极小值;
(2)若函数g(x)=x3+bx2-(2b+4)x+lnx(b∈R)的极小值点与f(x)的极小值点相同。求证:g(x)的极大值小于等于 .
.
 x3-
x3- x2+ax.
x2+ax.(1)当a=2时,求f(x)的极小值;
(2)若函数g(x)=x3+bx2-(2b+4)x+lnx(b∈R)的极小值点与f(x)的极小值点相同。求证:g(x)的极大值小于等于
 .
. 解:(1)当a=2时,f′(x)=x2-3x+2=(x-1)(x-2),
列表如下: 
所以,f(x)的极小值为f(2)=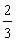 。
。
(2)f′(x)=x2-(a+1)x+a=(x-1)(x-a),
g′(x)=3x2+2bx-(2b+4)+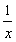 =
=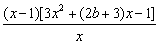 ,
,
令p(x)=3x2+(2b+3)x-1,
①当1<a≤2时,f(x)的极小值点x=a,
则g(x)的极小值点也为x=a,
所以,p(a)=0,即3a2+(2b+3)a-1=0,即b=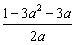 ,
,
此时,g(x)的极大值=g(1)=1+b-(2b+4)=-3-b=-3+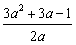 =
=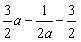 ,
,
由于1<a≤2,故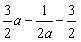 ≤
≤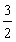 ×2-
×2-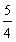 -
-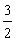 =
=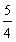 ;
;
②当0<a<1时,f(x)的极小值点x=1,则g(x)的极小值点为x=1,
由于p(x)=0有一正一负两实根,
不妨设x2<0<x1,所以0<x1<1,即p(1)=3+2b+3-1>0,故b>-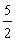 ,
,
此时g(x)的极大值点x=x1,
有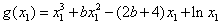
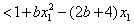
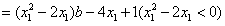
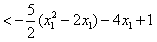
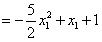
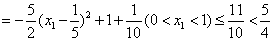
综上所述,g(x)的极大值小于等于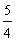 .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目