题目内容
f(x)是以4为周期的奇函数,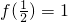 且
且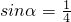 ,则f(4cos2α)=________.
,则f(4cos2α)=________.
-1
分析:根据题意,由sinα= ,结合余弦的二倍角公式可得cos2α=
,结合余弦的二倍角公式可得cos2α= ,则f(4cos2α)=f(
,则f(4cos2α)=f( ),结合函数的周期性与奇偶性可得f(
),结合函数的周期性与奇偶性可得f( )=f(-
)=f(- )=-f(
)=-f( ),由题意可得答案.
),由题意可得答案.
解答:根据题意,若sinα= ,则cos2α=1-2sin2α=
,则cos2α=1-2sin2α= ,
,
则f(4cos2α)=f( ),
),
f(x)是以4为周期的函数,则f( )=f(-
)=f(- )
)
又由函数f(x)为奇函数,则f(- )=-f(
)=-f( )=-1,
)=-1,
即有f(4cos2α)=f( )=f(
)=f( )=f(-
)=f(- )=-f(
)=-f( )=-1;
)=-1;
故答案为-1.
点评:本题考查函数的奇偶性与周期性的应用,涉及二倍角公式的应用,注意正确运用二倍角公式.
分析:根据题意,由sinα=
 ,结合余弦的二倍角公式可得cos2α=
,结合余弦的二倍角公式可得cos2α= ,则f(4cos2α)=f(
,则f(4cos2α)=f( ),结合函数的周期性与奇偶性可得f(
),结合函数的周期性与奇偶性可得f( )=f(-
)=f(- )=-f(
)=-f( ),由题意可得答案.
),由题意可得答案.解答:根据题意,若sinα=
 ,则cos2α=1-2sin2α=
,则cos2α=1-2sin2α= ,
,则f(4cos2α)=f(
 ),
),f(x)是以4为周期的函数,则f(
 )=f(-
)=f(- )
)又由函数f(x)为奇函数,则f(-
 )=-f(
)=-f( )=-1,
)=-1,即有f(4cos2α)=f(
 )=f(
)=f( )=f(-
)=f(- )=-f(
)=-f( )=-1;
)=-1;故答案为-1.
点评:本题考查函数的奇偶性与周期性的应用,涉及二倍角公式的应用,注意正确运用二倍角公式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目