题目内容
已知f(x)为二次函数,不等式f(x)+2<0的解集为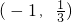 ,且对任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0.数列an满足a1=1,
,且对任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0.数列an满足a1=1,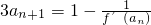 (n∈N×)
(n∈N×)
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设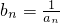 ,求数列bn的通项公式;
,求数列bn的通项公式;
(Ⅲ)若(Ⅱ)中数列bn的前n项和为Sn,求数列Sn•cos(bnπ)的前n项和Tn.
解:(Ⅰ)依题意,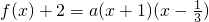 (a>0),
(a>0),
即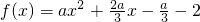
令 ,则sinα=1,cosβ=-1,有f(1)≤0,f(2-1)≥0,
,则sinα=1,cosβ=-1,有f(1)≤0,f(2-1)≥0,
得f(1)=0,即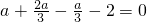 ,得
,得 .
.
∴ .-(4分)
.-(4分)
(Ⅱ)f'(x)=3x+1,则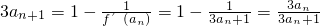
即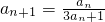 ,两边取倒数,得
,两边取倒数,得 ,即bn+1=3+bn.
,即bn+1=3+bn.
∴数列bn是首项为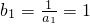 ,公差为3的等差数列.
,公差为3的等差数列.
∴bn=1+(n-1)•3=3n-2(n∈N*).(9分)
(Ⅲ)∵cos(bnπ)=cos(3n-2)π=cos(nπ)=(-1)n
∴Sn•cos(bnπ)=(-1)n•Sn∴Tn=-S1+S2-S3+S4-+(-1)nSn.
(1)当n为偶数时Tn=(S2-S1)+(S4-S3)++(Sn-Sn-1)=b2+b4++bn
=
(2)当n为奇数时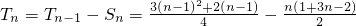 =
=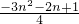
综上,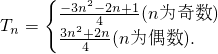 (13分)
(13分)
分析:(Ⅰ)根据“f(x)为二次函数,不等式f(x)+2<0的解集为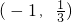 ,”可得到
,”可得到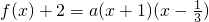 即
即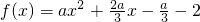 ,再由“任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0”可得f(1)≤0,f(2-1)≥0,从而有f(1)=0,解得
,再由“任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0”可得f(1)≤0,f(2-1)≥0,从而有f(1)=0,解得 得到函数的解析式.
得到函数的解析式.
(Ⅱ)先求导数f'(x)=3x+1,则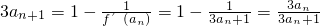 即
即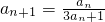 ,两边取倒数,有
,两边取倒数,有 由等差数列定义求解.
由等差数列定义求解.
(Ⅲ)化简得Sn•cos(bnπ)=(-1)n•Sn∴以有Tn=-S1+S2-S3+S4-+(-1)nSn.再分n为偶数和n为奇数两种情况化简即可.
点评:本题主要考查函数与数列的综合运用,主要涉及了二次函数求解析式,构造数列求数列的通项及前n项和等问题,属于中档题.
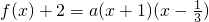 (a>0),
(a>0),即
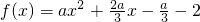
令
 ,则sinα=1,cosβ=-1,有f(1)≤0,f(2-1)≥0,
,则sinα=1,cosβ=-1,有f(1)≤0,f(2-1)≥0,得f(1)=0,即
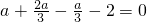 ,得
,得 .
.∴
 .-(4分)
.-(4分)(Ⅱ)f'(x)=3x+1,则
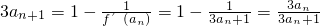
即
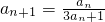 ,两边取倒数,得
,两边取倒数,得 ,即bn+1=3+bn.
,即bn+1=3+bn.∴数列bn是首项为
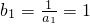 ,公差为3的等差数列.
,公差为3的等差数列.∴bn=1+(n-1)•3=3n-2(n∈N*).(9分)
(Ⅲ)∵cos(bnπ)=cos(3n-2)π=cos(nπ)=(-1)n
∴Sn•cos(bnπ)=(-1)n•Sn∴Tn=-S1+S2-S3+S4-+(-1)nSn.
(1)当n为偶数时Tn=(S2-S1)+(S4-S3)++(Sn-Sn-1)=b2+b4++bn
=

(2)当n为奇数时
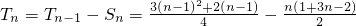 =
=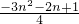
综上,
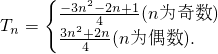 (13分)
(13分)分析:(Ⅰ)根据“f(x)为二次函数,不等式f(x)+2<0的解集为
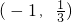 ,”可得到
,”可得到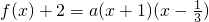 即
即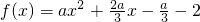 ,再由“任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0”可得f(1)≤0,f(2-1)≥0,从而有f(1)=0,解得
,再由“任意α,β∈R恒有f(sinα)≤0,f(2+cosβ)≥0”可得f(1)≤0,f(2-1)≥0,从而有f(1)=0,解得 得到函数的解析式.
得到函数的解析式.(Ⅱ)先求导数f'(x)=3x+1,则
 即
即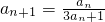 ,两边取倒数,有
,两边取倒数,有 由等差数列定义求解.
由等差数列定义求解.(Ⅲ)化简得Sn•cos(bnπ)=(-1)n•Sn∴以有Tn=-S1+S2-S3+S4-+(-1)nSn.再分n为偶数和n为奇数两种情况化简即可.
点评:本题主要考查函数与数列的综合运用,主要涉及了二次函数求解析式,构造数列求数列的通项及前n项和等问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目