题目内容
若a>0,b>0,a,b的等差中项是 ,且α=a+
,且α=a+ ,β=b+
,β=b+ ,则α+β的最小值为
,则α+β的最小值为
- A.2
- B.3
- C.4
- D.5
D
分析:a+b=1, =
= =1+
=1+ ,
, =
=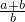 =
= +1,使用基本不等式可求最小值.
+1,使用基本不等式可求最小值.
解答:因为a,b的等差中项是 ,∴a+b=1,所以,α+β=a+
,∴a+b=1,所以,α+β=a+ +b+
+b+ =1+
=1+ +
+ =1+1+
=1+1+ +1+
+1+ ≥5,
≥5,
当且仅当a=b= 时,等号成立.
时,等号成立.
故选D
点评:本题考查等差数列的性质,基本不等式的应用,及1的代换.
分析:a+b=1,
 =
= =1+
=1+ ,
, =
=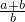 =
= +1,使用基本不等式可求最小值.
+1,使用基本不等式可求最小值.解答:因为a,b的等差中项是
 ,∴a+b=1,所以,α+β=a+
,∴a+b=1,所以,α+β=a+ +b+
+b+ =1+
=1+ +
+ =1+1+
=1+1+ +1+
+1+ ≥5,
≥5,当且仅当a=b=
 时,等号成立.
时,等号成立.故选D
点评:本题考查等差数列的性质,基本不等式的应用,及1的代换.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目