Question

【题目】数列{an}满足a1=2，an+1=an2+6an+6（n∈N×）
（1）设Cn=log5（an+3），求证{Cn}是等比数列；
（2）求数列{an}的通项公式；
（3）设bn= ﹣ ，数列{bn}的前n项和为Tn ， 求证：﹣ ≤Tn＜﹣ ．

Answer 1

【答案】
（1）解：由an+1=an2+6an+6得an+1+3=（an+3）2，

∴ =2 ，即cn+1=2cn

∴{cn}是以2为公比的等比数列．

（2）解：又c1=log55=1，

∴cn=2n﹣1，即 =2n﹣1，

∴an+3=

故an= ﹣3

（3）解：∵bn= ﹣ = ﹣ ，∴Tn= ﹣ =﹣ ﹣ ．

又0＜ = ．

∴﹣ ≤Tn＜﹣

【解析】（1）由已知可得，an+1+3=（an+3）2 ， 利用构造法令Cn=log5（an+3），则可得 ，从而可证数列{cn}为等比数列；（2）由（1）可先求数列cn ， 代入cn=log5（an+3）可求an；（3）把（2）中的结果代入整理可得， ，则代入Tn=b1+b2+…+bn相消可证
【考点精析】关于本题考查的等比关系的确定和数列的前n项和，需要了解等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断；数列{an}的前n项和sn与通项an的关系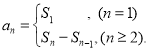才能得出正确答案．