题目内容
19. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
分析 由条件利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由函数f(x)=sin(ωx+φ)(ω>0,|ω|<$\frac{π}{2}$)的部分图象可得$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,
求得ω=2.
再把点($\frac{7π}{12}$,0)代入函数的解析式可得sin(2×$\frac{7π}{12}$+φ)=0,∴2×$\frac{7π}{12}$+φ=kπ,k∈z,
求得φ=kπ-$\frac{7π}{6}$,∴φ=-$\frac{π}{6}$,f(x)=sin(2x-$\frac{π}{6}$).
故把y=cos2x=sin(2x+$\frac{π}{2}$)的图象向右平移$\frac{π}{3}$个长度单位,
即可得到y=sin[2(x-$\frac{π}{3}$)+$\frac{π}{2}$]=sin(2x-$\frac{π}{6}$)的图象,
故选:A.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
7. 如图,是一个正方体的展开图,如果将它还原为正方体,那么AB、CD这两条线段所在直线的位置关系是( )
如图,是一个正方体的展开图,如果将它还原为正方体,那么AB、CD这两条线段所在直线的位置关系是( )
 如图,是一个正方体的展开图,如果将它还原为正方体,那么AB、CD这两条线段所在直线的位置关系是( )
如图,是一个正方体的展开图,如果将它还原为正方体,那么AB、CD这两条线段所在直线的位置关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 平行或异面 |
11.某程序框图如图所示,该程序运行后输出S的值是( )


| A. | $\frac{1}{3}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证: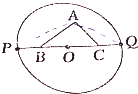 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.