题目内容
如下四个函数:
①f(x)=sinx②f(x)=x2+2x-1③f(x)=-x3+4x+2④f(x)=log
x
性质A:存在不相等的实数x1、x2,使得
=f(
)
性质B:对任意0<x2<x3<1,总有f(x1)<f(x2)
以上四个函数中同时满足性质A和性质B的函数个数为( )
①f(x)=sinx②f(x)=x2+2x-1③f(x)=-x3+4x+2④f(x)=log
| 1 |
| 2 |
性质A:存在不相等的实数x1、x2,使得
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
性质B:对任意0<x2<x3<1,总有f(x1)<f(x2)
以上四个函数中同时满足性质A和性质B的函数个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
分析:由于性质B,即单调性的检验更易于进行,所以先检验它们的单调性,其中函数f(x)=-x3+4x+2的单调性需用导数法判断;对于性质A,可结合奇函数的性质f(x)+f(-x)=0举出例证,其中函数f(x)=x2+2x-1需用反证法思想推出矛盾.则问题解决.
解答:解:(1)由性质B:“对任意0<x1<x2<1,总有f(x1)<f(x2)”知,函数f(x)在(0,1)上是增函数.
①∵f(x)=sinx在[0,
]上是增函数,∴f(x)=sinx在(0,1)上是增函数.
②∵f(x)=x2+2x-1在[-1,+∞)上是增函数,∴f(x)=x2+2x-1在(0,1)上是增函数.
③∵f′(x)=-3x2+4,且在(-
,
)上f′(x)>0,∴f(x)=-x3+4x+2在(-
,
)上是增函数,∴f(x)=-x3+4x+2在(0,1)上是增函数.
④∵f(x)=log
x在(0,+∞)上是减函数,∴f(x)=log
x在(0,1)上是减函数,而不是增函数.
所以排除④.
(2)性质A:存在不相等的实数x1、x2,使得
=f(
)
①对于f(x)=sinx,令x1=1,x2=-1,则
=
(sin1+sin(-1))=0,f(
)=f(0)=sin0=0,
∴f(x)=sinx满足性质A.
③对于f(x)=-x3+4x+2,令x1=1,x2=-1,则
=
×4=2,f(
)=f(0)=2,
∴f(x)=-x3+4x+2满足性质A.
②对于f(x)=x2+2x-1,假设存在不相等的实数x1、x2,使得
=f(
)
则有
(x12+2x1-1+x22+2x2-1)=(
)2+(x1+x2)-1
化简得(x1-x2)2=0,即x1=x2,这与x1≠x2矛盾.
∴f(x)=x2+2x-1不满足性质A.
所以只有①③同时满足性质A和性质B.
故选B.
①∵f(x)=sinx在[0,
| π |
| 2 |
②∵f(x)=x2+2x-1在[-1,+∞)上是增函数,∴f(x)=x2+2x-1在(0,1)上是增函数.
③∵f′(x)=-3x2+4,且在(-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
④∵f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
所以排除④.
(2)性质A:存在不相等的实数x1、x2,使得
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
①对于f(x)=sinx,令x1=1,x2=-1,则
| f(x1)+f(x2) |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
∴f(x)=sinx满足性质A.
③对于f(x)=-x3+4x+2,令x1=1,x2=-1,则
| f(x1)+f(x2) |
| 2 |
| 1 |
| 2 |
| x1+x2 |
| 2 |
∴f(x)=-x3+4x+2满足性质A.
②对于f(x)=x2+2x-1,假设存在不相等的实数x1、x2,使得
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
则有
| 1 |
| 2 |
| x1+x2 |
| 2 |
化简得(x1-x2)2=0,即x1=x2,这与x1≠x2矛盾.
∴f(x)=x2+2x-1不满足性质A.
所以只有①③同时满足性质A和性质B.
故选B.
点评:本题需要检验的方面较多,相对比较麻烦,对学生的意志力提出了更高的要求;还应注意:证明存在性问题成立,只需举出一个例子即可;但要证明存在性问题不成立,需严格的逻辑推理.

练习册系列答案
相关题目
 某程序框图如图所示,现输入如下四个函数:f(x)=sinx,f(x)=x2,f(x)=
某程序框图如图所示,现输入如下四个函数:f(x)=sinx,f(x)=x2,f(x)=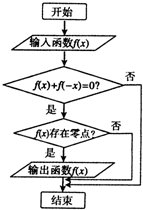 (2012•淄博一模)某程序框图如图所示,现输入如下四个函数:f(x)=x2,
(2012•淄博一模)某程序框图如图所示,现输入如下四个函数:f(x)=x2,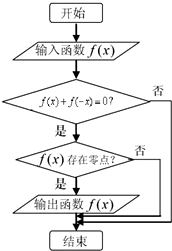 程序框图如图所示,现输入如下四个函数:
程序框图如图所示,现输入如下四个函数: 执行如图所示的程序框图,若每次分别输入如下四个函数:
执行如图所示的程序框图,若每次分别输入如下四个函数: