题目内容
已知函数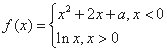 ,其中
,其中 是实数.设
是实数.设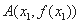 ,
, 为该函数图象上的两点,且
为该函数图象上的两点,且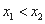 .
.
(Ⅰ)指出函数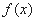 的单调区间;
的单调区间;
(Ⅱ)若函数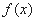 的图象在点
的图象在点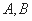 处的切线互相垂直,且
处的切线互相垂直,且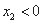 ,证明:
,证明: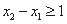 ;
;
(Ⅲ)若函数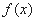 的图象在点
的图象在点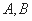 处的切线重合,求
处的切线重合,求 的取值范围.
的取值范围.
【答案】解:(Ⅰ)函数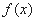 的单调减区间为
的单调减区间为 ,单调增区间为
,单调增区间为 ,
,
(Ⅱ)由导数的几何意义知,点A处的切线斜率为 ,点B处的切线斜率为
,点B处的切线斜率为 ,
,
故当点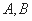 处的切线互相垂直时,有
处的切线互相垂直时,有
 ,
,
当x<0时,
因为 ,所以
,所以  ,所以
,所以 ,
, ,
,
因此 ,
,
(当且仅当 ,即
,即 且
且 时等号成立)
时等号成立)
所以函数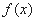 的图象在点
的图象在点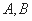 处的切线互相垂直时有
处的切线互相垂直时有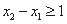 .
.
(Ⅲ)当 或
或 时,
时,
 ,故
,故 .
.
当 时,
时,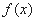 的图象在点
的图象在点 处的切线方程为
处的切线方程为
 即
即  .
.
当 时,
时,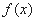 的图象在点
的图象在点 处的切线方程为
处的切线方程为
 即
即  .
.


练习册系列答案
相关题目
 的方程为
的方程为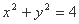 ,过点
,过点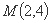 作圆
作圆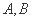 ,直线
,直线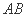 恰好经过椭圆
恰好经过椭圆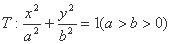 的右顶点和上顶点。
的右顶点和上顶点。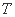 的方程;
的方程;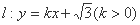 与椭圆相交于
与椭圆相交于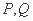 两点,
两点,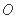 为坐标原点,求
为坐标原点,求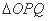 面积的最大值.
面积的最大值. ,则
,则 =
=  有两个极值点
有两个极值点 ,若
,若 ,则关于
,则关于 的方
的方  的不同实根个数为 ( )
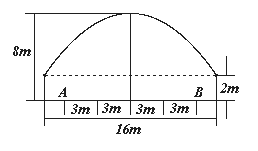
的不同实根个数为 ( ) ,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到
,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 .(精确到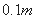 )
) 
 的最小值为(
的最小值为(  )
) B.
B. C.
C. D.
D.
 使函数
使函数 是奇函数。
是奇函数。 ;(2)
;(2) 。
。 ,且
,且 的终边过点
的终边过点 ,则
,则 =_____。
=_____。