题目内容
已知f（x）=
，求（1）f（x）的周期；
（2）函数f（x）的值域．
解：（1）函数f（x）的定义域为{x|x≠，k∈Z}，
f（x）=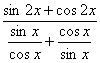
=sinxcosx（sin2x+cos2x）
=
（sin22x+sin2xcos2x）
=
（
+
sin4x）
=
（sin4x-cos4x+1）
=
sin（4x-
）+
，
函数f（x）的周期为T=
=
.
（2）由x≠
，k∈Z，得4x-
≠-
+2kπ，k∈Z.
此时，y≠
sin（-
+2kπ）+
=0，即y≠0.
但当4x-
=
+2kπ，即x=
+
，k∈Z时，y=
sin（
+2kπ）+
=0成立.
∴sin（4x-
）仍能取满[-1，1]上的每一个值.
∴f（x）的值域为[
，
].
练习册系列答案
相关题目
，求f（x）．
，求f（x）．
，求f（x）．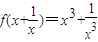
，求f（x）．
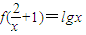，求f（x）．
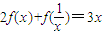，求f（x）．
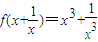，求f（x）．
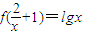，求f（x）．
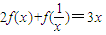，求f（x）．