题目内容
在△ABC中,a,b,c分别为角A、B、C的对边,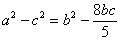 ,a=3,△ABC的面积为6,D为
,a=3,△ABC的面积为6,D为
△ABC内任一点,点D到三边距离之和为d。
(1)求角A的正弦值;
(2)求边b、c;
(3)求d的取值范围。
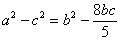 ,a=3,△ABC的面积为6,D为
,a=3,△ABC的面积为6,D为△ABC内任一点,点D到三边距离之和为d。
(1)求角A的正弦值;
(2)求边b、c;
(3)求d的取值范围。
解:(1)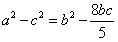 ,
,
∴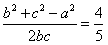 ,
,
即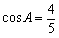 ,
,
∴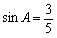 。
。
(2)∵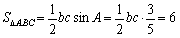 ,
,
∴bc=20,
由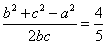 及bc=20,a=3,
及bc=20,a=3,
解得b=4,c=5或b=5,c= 4。
(3)设D到三边的距离分别为x、y、z,
则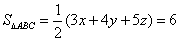 ,
,
∴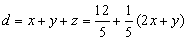 ,
,
又x、y满足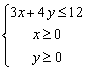 ,
,
画出不等式表示的平面区域得,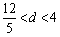 。
。
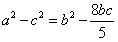 ,
,∴
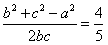 ,
,即
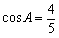 ,
,∴
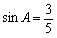 。
。(2)∵
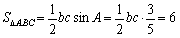 ,
,∴bc=20,
由
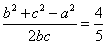 及bc=20,a=3,
及bc=20,a=3,解得b=4,c=5或b=5,c= 4。
(3)设D到三边的距离分别为x、y、z,
则
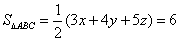 ,
,∴
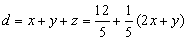 ,
,又x、y满足
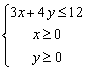 ,
,画出不等式表示的平面区域得,
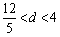 。
。
练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|