题目内容
已知某四面体的六条棱长分别为 ,
, ,
, ,
, ,
, ,
, ,则两条较长棱所在直线所成角的余弦值为________.
,则两条较长棱所在直线所成角的余弦值为________.

分析:当较长的两条棱是四面体相对的棱时,根据三角形两边之和大于第三边出现矛盾,得此种情况不存在;当它们是四面体相邻的棱时,根据余弦定理可以算出所成角的余弦之值,由此可得正确答案.
解答:①当较长的两条棱是四面体相对的棱时,

如图中的左图,取CD中点E,则
∵等腰△BCD中,中线BE⊥CD,等腰△ACD中,中线AE⊥CD,
AE、BE是平面ABE内的相交直线
∴CD⊥平面ABE,结合AB⊆平面ABE,可得AB⊥CD
此时两条较长棱所在直线所成角的余弦值为cos90°=0,
检验:此时△ABE中,AE=BE=
 ,不满足AE+BE>AB,
,不满足AE+BE>AB,故此种情况舍去;
②当较长的两条棱是四面体相邻的棱时,如图中的右图
设所成的角为θ,根据余弦定理得cosθ=
 =
=
综上所述,得所求余弦值为0或

故答案为:

点评:本题在四面体中求两条棱所在直线所成角的余弦值,着重考查了余弦定理、线面垂直的判定与性质和异面直线所成角等知识,属于基础题.

练习册系列答案
相关题目
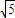 ,
,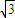 ,
,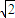 ,
,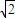 ,
,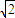 ,
,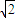 ,则两条较长棱所在直线所成角的余弦值为 .
,则两条较长棱所在直线所成角的余弦值为 .