题目内容
数列{an}中，a1=1，3•an•an-1+an-an-1=0（n≥2，n∈N*），则a10=________．
分析：将3•an•an-1+an-an-1=0移向两边同除以an•an-1 得
，判断出数列{
}是等差数列，求出，得出an再求a10．解答：将3•an•an-1+an-an-1=0移向 两边同除以an•an-1 得
∴数列{
}是以3为公差，以1为首项的等差数列，∴=1+（n-1）×3=3n-2，∴an=
，a10=
故答案为
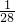．点评：本题考查等差数列的判定、通项公式求解．考查转化构造、计算能力．
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
数列{an}中，a1=
，an+an+1=
，n∈N*，则
（a1+a2+…+an）等于（ ）
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|