题目内容
(本小题满分12分)
如图所示,在正方体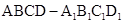 中,E是棱
中,E是棱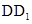 的中点.
的中点.
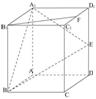
(Ⅰ)求直线BE与平面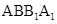 所成的角的正弦值;
所成的角的正弦值;
(Ⅱ)在棱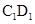 上是否存在一点F,使
上是否存在一点F,使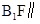 平面
平面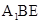 ?证明你的结论.
?证明你的结论.
【答案】
解法1:设正方体的棱长为1.如图所示,以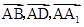 为单位正交基底建立空间直角坐标系.
为单位正交基底建立空间直角坐标系.
(Ⅰ)依题意,
得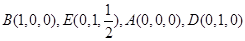 ,
,
所以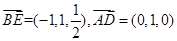 .
.
在正方体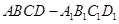 中,因为
中,因为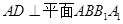 ,所以
,所以 是平面
是平面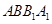 的一个法向量,设直线BE和平面
的一个法向量,设直线BE和平面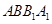 所成的角为
所成的角为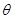 ,则
,则
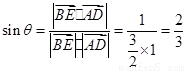 .
.
即直线BE和平面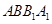 所成的角的正弦值为
所成的角的正弦值为 .
.

设F是棱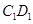 上的点,则
上的点,则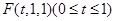 .又
.又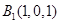 ,所以
,所以
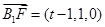 .而
.而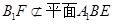 ,于是
,于是
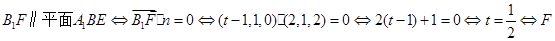 为
为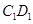 的中点,这说明在棱
的中点,这说明在棱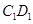 上存在点F(
上存在点F(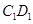 的中点),使
的中点),使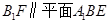 .[来源:ZXXK]
.[来源:ZXXK]
解法2:(Ⅰ)如图(a)所示,取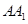 的中点M,连结EM,BM.因为E是
的中点M,连结EM,BM.因为E是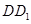 的中点,四边形
的中点,四边形 为正方形,所以EM∥AD.
为正方形,所以EM∥AD.

即直线BE和平面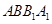 所成的角的正弦值为
所成的角的正弦值为 .
.

(Ⅱ)在棱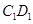 上存在点F,使
上存在点F,使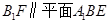 .
.
事实上,如图(b)所示,分别取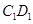 和CD的中点F,G,连结
和CD的中点F,G,连结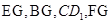 .因
.因 ,且
,且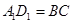 ,所以四边形
,所以四边形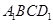 是平行四边形,因此
是平行四边形,因此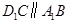 .又E,G分别为
.又E,G分别为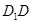 ,CD的中点,所以
,CD的中点,所以 ,从而
,从而 .这说明
.这说明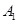 ,B,G,E共面,所以
,B,G,E共面,所以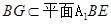 .
.
因四边形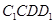 与
与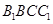 皆为正方形,F,G分别为
皆为正方形,F,G分别为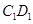 和CD的中点,所以
和CD的中点,所以
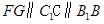 ,且
,且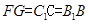 ,因此四边形
,因此四边形 是平行四边形,所以
是平行四边形,所以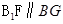 .而
.而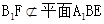 ,
,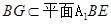 ,故
,故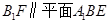 .
.
【解析】略

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目