Question

已知△ABC是正三角形,PA⊥平面ABC,且PA=AB=a,求二面角A-PC-B的大小.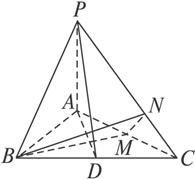

图2-3-12

Answer 1

思路分析:要求二面角的大小,首先要在图形中构造出二面角的平面角,然后利用其平面角度量二面角的大小.过棱上一点,分别在两个面内作或证棱的垂线,即可产生二面角的平面角,要充分利用三角函数定义求得具体值.

解:取AC的中点M,连结BM,作MN⊥PC于N,连结BN(如图2-3-12).

∵PA⊥平面ABC,∴平面PAC⊥平面ABC.

易证BM⊥AC,AC=平面PAC∩平面ABC.

∴BM⊥平面PAC(面面垂直的性质).

∵MN⊥PC,∴NB⊥PC.

∴∠MNB是二面角A-PC-B的平面角.

易知MN=a,BM=a.

∴tan∠MNB=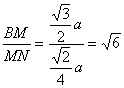.∴∠MNB=arctan,即二面角A-PC-B的大小为arctan.

  绿色通道:度量二面角的大小是通过其平面角进行,所以在图形中构造出二面角的平面角,就能将空间问题转化为平面问题,利用直角三角形中,锐角三角函数定义,有些问题也可用斜三角形中的直角三角形加以处理.求α-l-β的二面角时,通常在其中的一个半平面内找一点A,作另一个半平面的垂线,垂足为B,然后过A(或B)作l的垂线,垂足为C,连结BC(或AC),则∠ACB即为所求.