Question

已知正方形ABCD的边长为4，E、F分别是AB、AD的中点，GC⊥平面ABCD，且GC=2，则点B到平面EFG的距离为（ ）
A．
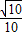
B．
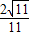
C．
D．1

Answer 1

【答案】分析：利用题设条件推导出BD∥平面EFG，从而得到BD和平面EFG的距离就是点B到平面EFG的距离，作OK⊥HG交HG于点K，由两平面垂直的性质定理知OK⊥平面EFG，所以线段OK的长就是点B到平面EFG的距离．
解答：解：如图，连接EG、FG、EF、BD、AC、EF、BD分别交AC于H、O．
因为ABCD是正方形，E、F分别为AB和AD的中点，故EF∥BD，H为AO的中点．
由直线和平面平行的判定定理知BD∥平面EFG，
所以BD和平面EFG的距离就是点B到平面EFG的距离．
∵BD⊥AC，∴EF⊥HC．
∵GC⊥平面ABCD，∴EF⊥GC，
∵HC∩GC=C，∴EF⊥平面HCG．
∵EF?平面EFG，∴平面EFG⊥平面HCG，HG是这两个垂直平面的交线．
作OK⊥HG交HG于点K，由两平面垂直的性质定理知OK⊥平面EFG，
所以线段OK的长就是点B到平面EFG的距离．
∵正方形ABCD的边长为4，GC=2，
∴AC=4，HO=，HC=3．
∴在Rt△HCG中，HG==．
由于Rt△HKO和Rt△HCG有一个锐角是公共的，
故Rt△HKO∽△HCG．
∴OK===．
即点B到平面EFG的距离为．
故选B．
点评：本小题主要考查直线与平面的位置关系、平面与平面的位置关系、点到平面的距离等有关知识，考查学生的空间想象能力和思维能力，属于中档题．解决此类问题应该注意从三维空间向二维平面的转化，从而找到解题的捷径．