题目内容
是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,说明a可取哪些值;如果不存在,请说明理由.
解析:假设存在实数a,分a>1,0<a<1两种情况,由复合函数单调性求解.
设g(x)=ax2-x,假设符合条件的a值存在.
当a>1时,为使函数y=f(x)=loga(ax2-x)在闭区间[2,4]上是增函数,只需g(x)=ax2-x在[2,4]上是增函数,故应满足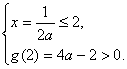 解得a>
解得a>![]() ,
,
又a>1,∴a>1.
当0<a<1时,为使函数y=f(x)=loga(ax2-x)在闭区间[2,4]上是增函数,只需g(x)=ax2-x在[2,4]上是减函数.
故应满足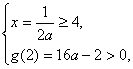 此不等式组无解.
此不等式组无解.
综上,可知当a∈(1,+∞)时,f(x)=loga(ax2-x)在[2,4]上为增函数.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
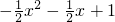 ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;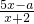 在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.
在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.