题目内容
设A={x|2x2-px+q=0}，B={x|6x2+（p+2）x+5+q=0}，若A∩B={
}，则A∪B=（ ）A．{
}B．{
，
}C．{
，
，-2}D．{
，
，-4}
【答案】分析：由A={x|2x2-px+q=0}，B={x|6x2+（p+2）x+5+q=0}，A∩B={
}，知
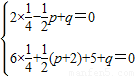，解得p=-7，q=-4，由此能求出A∪B．
解答：解：∵A={x|2x2-px+q=0}，B={x|6x2+（p+2）x+5+q=0}，A∩B={
}，
∴
，
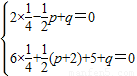解得p=-7，q=-4，
∴A={x|2x2+7x-4=0}={-4，
}，
B={x|6x2-5x+1=0}={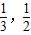
}，
∴A∪B={
，
，-4}．
故选D．
点评：本题考查集合的交、并、补集的混合运算，是基础题．解题时要认真审题，仔细解答．
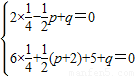}，知，解得p=-7，q=-4，由此能求出A∪B．解答：解：∵A={x|2x2-px+q=0}，B={x|6x2+（p+2）x+5+q=0}，A∩B={
}，∴
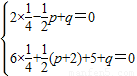，解得p=-7，q=-4，
∴A={x|2x2+7x-4=0}={-4，
}，B={x|6x2-5x+1=0}={
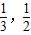}，∴A∪B={
，，-4}．故选D．
点评：本题考查集合的交、并、补集的混合运算，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目