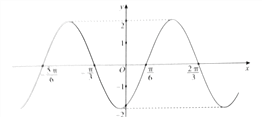
题目内容
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点?若过定点则求出该定点,若不存在则说明理由;
是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为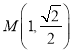 ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)若直线l与圆O交于不同的两点A,B,当![]() 时,点O到l的距离
时,点O到l的距离![]() ,由此求k的值;
,由此求k的值;
(2)求出直线CD的方程,即可,探究:直线CD是否过定点;
(3)求出四边形EGFH的面积,利用配方法,求出最大值.
试题解析:
(1)![]() 点
点![]() 到
到![]() 的距离
的距离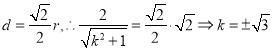 .
.
(2)由题意可知: ![]() 四点共圆且在以
四点共圆且在以![]() 为直径的圆上,设
为直径的圆上,设![]() .
.
其方程为: ![]() ,
,
即![]() ,
,
又![]() 在圆
在圆![]() 上
上
![]() ,即
,即![]() ,
,
由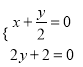 ,得
,得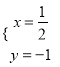
![]() 直线
直线![]() 过定点
过定点![]() .
.
(3)设圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() .
.
则![]() ,
,
![]() .
.
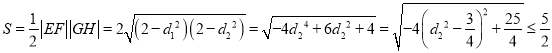 .
.
当且仅当![]() ,即
,即![]() 时,取“
时,取“![]() ”
”
![]() 四边形
四边形![]() 的面积的最大值为
的面积的最大值为![]() .
.

 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如表:
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值k= ![]() ≈4.844,因为k≥3.841,根据下表中的参考数据:
≈4.844,因为k≥3.841,根据下表中的参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为( )
A.95%
B.50%
C.25%
D.5%
【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.