题目内容
平面直角坐标系中,O为坐标原点,已知两定点A(1,0),B(0,-1),动点P(x,y)满足:(1)求点P的轨迹方程;
(2)设点P的轨迹与双曲线C:![]() =1(a>0,b>0)交于相异两点M、N,若以MN为直径的圆经过原点,且双曲线C的离心率等于
=1(a>0,b>0)交于相异两点M、N,若以MN为直径的圆经过原点,且双曲线C的离心率等于![]() ,求双曲线C的方程.
,求双曲线C的方程.
解:(1)由已知(x,y)=m(1,0)+(m-1)(0,-1),
∴![]() ∴x+y=1,即点P的轨迹方程为x+y-1=0.
∴x+y=1,即点P的轨迹方程为x+y-1=0.
(2)由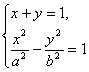 得(b2-a2)x2+2a2x-a2-a2b2=0.
得(b2-a2)x2+2a2x-a2-a2b2=0.
∵点P轨迹与双曲线C交于相异两点M,N,
∴b2-a2≠0,且Δ=4a2-4(b2-a2)(-a2-a2b2)>0,(*)设M(x1,y1),N(x2,y2),则
x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∵以MN为直径的圆经过原点,∴![]() ·
·![]() =0,即x1x2+y1y2=0.
=0,即x1x2+y1y2=0.
∴x1x2+(1-x1)(1-x2)=0,得1+![]() =0,即b2-a2-2a2b2=0. ①
=0,即b2-a2-2a2b2=0. ①
∴e=![]() .∴e2=
.∴e2=![]() =3.∴b2=2a2.②∴由①②解得a=
=3.∴b2=2a2.②∴由①②解得a=![]() ,b=
,b=![]() .
.
经检验a=![]() ,b=
,b=![]() 符合(*)式,∴双曲线C的方程为4x2-2y2=1.
符合(*)式,∴双曲线C的方程为4x2-2y2=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
平面直角坐标系中,O为坐标原点,已知两点A(3,1)、B(-1,3),若点C满足
=α
+β
,其中α、β∈R,且α+β=1,则点C的轨迹方程为( )
| OC |
| OA |
| OB |
| A、3x+2y-11=0 |
| B、(x-1)2+(y-2)2=5 |
| C、2x-y=0 |
| D、x+2y-5=0 |
 已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为
已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为