题目内容
在四棱锥P—ABCD中,底面ABCD是一直角梯形, ,
, 与底面成30°角。
与底面成30°角。
(1)若 为垂足,求证:
为垂足,求证: ;
;
(2)在(1)的条件下,求异面直线AE与CD所成角的余弦值;
(3)求平面PAB与平面PCD所成的锐二面角的正切值。

 ,
, 与底面成30°角。
与底面成30°角。(1)若
 为垂足,求证:
为垂足,求证: ;
;(2)在(1)的条件下,求异面直线AE与CD所成角的余弦值;
(3)求平面PAB与平面PCD所成的锐二面角的正切值。

(1)如图建立空间直角坐标系,



 ……3分
……3分
(2)
∴异面直线AE与CD所成角的余弦值为 . ……8分
. ……8分
(3)易知, 则
则 的法向量。
的法向量。

 ,
,







∴平面PAB与平面PCD所成二面角的正切值为2。



 ……3分
……3分(2)

∴异面直线AE与CD所成角的余弦值为
 . ……8分
. ……8分(3)易知,
 则
则 的法向量。
的法向量。
 ,
,






∴平面PAB与平面PCD所成二面角的正切值为2。
略

练习册系列答案
相关题目
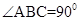 ,
,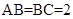 ,二面角P-AB-C为
,二面角P-AB-C为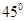 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.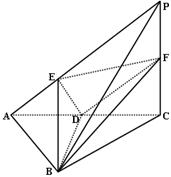
 B.
B.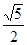 C.
C. D.
D.
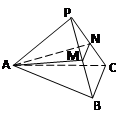
 中,
中, 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为  —
— —β的大小为45°,m,n为异面直线,且m
—β的大小为45°,m,n为异面直线,且m ,n
,n β,则m,n所成角的大小为
β,则m,n所成角的大小为 中,
中, 为顶点在底面上的射影,且
为顶点在底面上的射影,且 ,则直线
,则直线 与平面
与平面 所成角的大小等于
所成角的大小等于  在平面
在平面 外,
外, ,
, ,
, 、
、 分别是
分别是 和
和 的中点,则
的中点,则 的长是( )
的长是( )


