题目内容
己知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,A1、A2是椭圆的左右顶点,B1、B2是椭圆的上下顶点,四边形A1B1A2B2的面积为16
,A1、A2是椭圆的左右顶点,B1、B2是椭圆的上下顶点,四边形A1B1A2B2的面积为16 .
.
(1)求椭圆C的方程;
(2)圆M过A1、B1两点.当圆心M与原点O的距离最小时,求圆M的方程.
解:(1)依题意有: ①…(2分)
①…(2分)
四边形A1B1A2B2是以椭圆C的四顶点为顶点的菱形
可得:SA1B1A2B2= 即
即 ②…(4分)
②…(4分)
由①、②联解,可得:
所以椭圆C的方程为: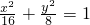 …(6分)
…(6分)
(2)依题意得
可得A1B1的中点为(-2, ),A1B1的斜率k=
),A1B1的斜率k=
∴A1B1的垂直平分线l的斜率为k'=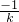 =-
=- ,
,
可得A1B1的垂直平分线l的方程为:y- =-
=- (x+2),化简得
(x+2),化简得 …③(8分)
…③(8分)
根据圆M过A1、B1两点,可得圆心M在l上,当圆心M与原点O的距离最小时,OM⊥l
∴OM的方程为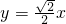 …④(10分)
…④(10分)
联立③、④得 ,得到
,得到 …(12分)
…(12分)
由此可得 ,
,
因此,此时的圆M方程为: …(14分)
…(14分)
分析:(1)根据椭圆的离心率和菱形A1B1A2B2的面积,建立关于a、b、c的方程组,解之可得 ,从而得到椭圆C的方程;
,从而得到椭圆C的方程;
(2)根据题意,过A1、B1两点的圆的圆心M在A1B1的垂直平分线l上,且当OM⊥l时圆心M与原点O的距离最小.由此得到直线OM的方程与直线l方程联解得到M(- ,-
,- ),再由MA1长得到圆M的半径,得到此时圆M的方程.
),再由MA1长得到圆M的半径,得到此时圆M的方程.
点评:本题给出椭圆满足的条件,求椭圆的方程并且求圆心M与原点距离最小时的圆M的方程,着重了椭圆的标准方程和简单几何性质、圆的标准方程等知识,属于中档题.
 ①…(2分)
①…(2分)四边形A1B1A2B2是以椭圆C的四顶点为顶点的菱形
可得:SA1B1A2B2=
 即
即 ②…(4分)
②…(4分)由①、②联解,可得:

所以椭圆C的方程为:
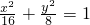 …(6分)
…(6分)(2)依题意得

可得A1B1的中点为(-2,
 ),A1B1的斜率k=
),A1B1的斜率k=
∴A1B1的垂直平分线l的斜率为k'=
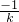 =-
=- ,
,可得A1B1的垂直平分线l的方程为:y-
 =-
=- (x+2),化简得
(x+2),化简得 …③(8分)
…③(8分)根据圆M过A1、B1两点,可得圆心M在l上,当圆心M与原点O的距离最小时,OM⊥l
∴OM的方程为
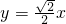 …④(10分)
…④(10分)联立③、④得
 ,得到
,得到 …(12分)
…(12分)由此可得
 ,
,因此,此时的圆M方程为:
 …(14分)
…(14分)分析:(1)根据椭圆的离心率和菱形A1B1A2B2的面积,建立关于a、b、c的方程组,解之可得
 ,从而得到椭圆C的方程;
,从而得到椭圆C的方程;(2)根据题意,过A1、B1两点的圆的圆心M在A1B1的垂直平分线l上,且当OM⊥l时圆心M与原点O的距离最小.由此得到直线OM的方程与直线l方程联解得到M(-
 ,-
,- ),再由MA1长得到圆M的半径,得到此时圆M的方程.
),再由MA1长得到圆M的半径,得到此时圆M的方程.点评:本题给出椭圆满足的条件,求椭圆的方程并且求圆心M与原点距离最小时的圆M的方程,着重了椭圆的标准方程和简单几何性质、圆的标准方程等知识,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点. =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线. +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点. =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线. +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点. =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线. +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点. =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线. +
+ =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点. =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.