题目内容
已知函数 ,且f(4)=3
,且f(4)=3(1)求m的值;
(2)证明f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.
【答案】分析:(1)据f(4)=3求出待定系数m的值.
(2)先看函数的定义域是否关于原点对称,再看f(x)与f(-x)的关系,依据奇偶性的定义进行判断.
(3)在(0,+∞)上任取x1>x2>0,计算对应的函数值之差,把此差变形为因式之积的形式,然后判断符号,比较f(x1)与
f(x2)的大小,得出结论.
解答:解:(1)∵f(4)=3,∴ ,∴m=1.(2分)
,∴m=1.(2分)
(2)因为 ,定义域为{x|x≠0},关于原点成对称区间.(3分)
,定义域为{x|x≠0},关于原点成对称区间.(3分)
又 ,(5分)
,(5分)
所以f(x)是奇函数.(6分)
(3)设x1>x2>0,则 (9分)
(9分)
因为x1>x2>0,所以x1-x2>0, ,(11分)
,(11分)
所以f(x1)>f(x2),因此f(x)在(0,+∞)上为单调增函数.
点评:本题考查用待定系数法求函数解析式,以及判断函数单调性、奇偶性的方法.
(2)先看函数的定义域是否关于原点对称,再看f(x)与f(-x)的关系,依据奇偶性的定义进行判断.
(3)在(0,+∞)上任取x1>x2>0,计算对应的函数值之差,把此差变形为因式之积的形式,然后判断符号,比较f(x1)与
f(x2)的大小,得出结论.
解答:解:(1)∵f(4)=3,∴
 ,∴m=1.(2分)
,∴m=1.(2分)(2)因为
 ,定义域为{x|x≠0},关于原点成对称区间.(3分)
,定义域为{x|x≠0},关于原点成对称区间.(3分)又
 ,(5分)
,(5分)所以f(x)是奇函数.(6分)
(3)设x1>x2>0,则
 (9分)
(9分)因为x1>x2>0,所以x1-x2>0,
 ,(11分)
,(11分)所以f(x1)>f(x2),因此f(x)在(0,+∞)上为单调增函数.
点评:本题考查用待定系数法求函数解析式,以及判断函数单调性、奇偶性的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
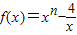 ,且f(4)=3.
,且f(4)=3.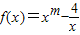 ,且f(4)=3
,且f(4)=3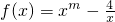 ,且f(4)=3.判断f(x)在(0,+∞)上的单调性,并给予证明;
,且f(4)=3.判断f(x)在(0,+∞)上的单调性,并给予证明;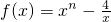 ,且f(4)=3.
,且f(4)=3.