题目内容
已知x∈R,f(x)是4x,x+2,-2x+4三者中的最小值,求f(x)的最大值.
解:由![]() 得它们的交点为A(
得它们的交点为A(![]() ,
,![]() ),而点A满足y=-2x+4.
),而点A满足y=-2x+4.
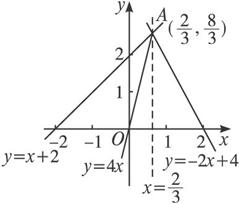
∴三条直线y=4x,y=x+2,y=-2x+4交于一点.在同一坐标系中,分别作出三条直线y=4x,y=x+2,y=-2x+4的图象,它们都交于一点(![]() ,
,![]() ).
).
在x≥![]() 所表示的平面区域中,三者最小值f(x)=-2x+4,在此区域内它的最大值为
所表示的平面区域中,三者最小值f(x)=-2x+4,在此区域内它的最大值为![]() .
.
∴f(x)的最大值为![]() .在x≤
.在x≤![]() 所表示的平面区域中,三者最小值f(x)=4x,在此区域内,它的最大值为
所表示的平面区域中,三者最小值f(x)=4x,在此区域内,它的最大值为![]() .
.
∴f(x)的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 R),
R), =
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数.
=
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数. ,若h (x)为偶函数,求
,若h (x)为偶函数,求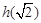 ;
; ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;